题目内容
3.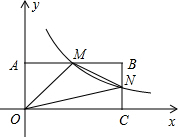 如图,在直角坐标系中,矩形OABC的顶点O是坐标原点,A,C分别在坐标轴上,点B的坐标为(4,2),M,N分别是AB,BC上的点,反比例函数y=$\frac{k}{x}$的图象经过点M,N.
如图,在直角坐标系中,矩形OABC的顶点O是坐标原点,A,C分别在坐标轴上,点B的坐标为(4,2),M,N分别是AB,BC上的点,反比例函数y=$\frac{k}{x}$的图象经过点M,N.(1)请用含k的式子表示出点M、N的坐标;
(2)若直线MN的解析式为y=-$\frac{1}{2}$x+3,求反比例函数的解析式;
(3)在(2)的条件下,若点P在x轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
分析 (1)由点B的坐标可得出M点的纵坐标和N点的横坐标,分别将y=2、x=4代入反比例解析式中,即可求出M点的横坐标以及N点的纵坐标,由此即可得出结论;
(2)将点M的坐标代入到直线MN的解析式中,可得到关于k的一元一次方程,解方程即可求出k的值;
(3)通过分割矩形OABC以及三角形的面积公式即可得到线段OP的长度,由OP的长度即可得出点P的坐标.
解答 解:(1)∵点B的坐标为(4,2),四边形OABC是矩形,
∴OA=BC=2,OC=AB=4.
将y=2代入y=$\frac{k}{x}$得:2=$\frac{k}{x}$,
解得:x=$\frac{k}{2}$,
∴点M($\frac{k}{2}$,2);
将x=4代入y=$\frac{k}{2}$得:y=$\frac{k}{4}$,
∴点N(4,$\frac{k}{2}$).
(2)∵点M($\frac{k}{2}$,2)在直线y=-$\frac{1}{2}$x+3上,
∴2=-$\frac{1}{2}$×$\frac{k}{2}$+3,解得:k=4,
∴反比例函数的解析式为y=$\frac{4}{x}$.
(3)由题意可得:
SBMON=S矩形OABC-S△AOM-S△CON=4×2-$\frac{1}{2}$×4-$\frac{1}{2}$×4=4.
S△OPM=$\frac{1}{2}$OP•AO=4,
∴OP=4,
∴点P的坐标为(4,0)或(-4,0).
点评 本题考查了反比例函数与一次函数交点的问题、三角形的面积公式以及反比例函数系数k的几何意义,解题的关键是:(1)分别将x=4、y=2代入反比例函数中;(2)解关于k的一元一次方程;(3)分割图形求面积.本题属于基础题,难度不大,解决该题型题目时,通过分割图形找出面积再结合三角形的面积公式得出线段的长度是关键.

 互动英语系列答案
互动英语系列答案| A. | 1 | B. | -1 | C. | 2a-1 | D. | -4027 |
| A. | 0.518×104 | B. | 5.18×105 | C. | 51.8×106 | D. | 518×103 |
| A. | -3 | B. | 0.5 | C. | 0 | D. | 4 |
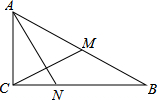 如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )
如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
| A. | 1.26×106 | B. | 12.6×104 | C. | 1.26×105 | D. | 0.126×106 |