题目内容
2.如图,点O是圆形纸片的圆心,将这个圆形纸片按下列顺序折叠,使$\widehat{AB}$和$\widehat{AC}$都经过圆心O,则阴影部分的面积是⊙O面积的$\frac{1}{3}$.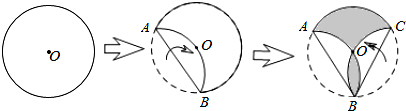
分析 作OD⊥AB于点D,连接AO,BO,CO,求出∠OAD=30°,得出∠AOC=120°,得出阴影部分的面积=S扇形AOC=⊙O面积的$\frac{1}{3}$,即可得出结果.
解答 解:作OD⊥AB于点D,连接AO,BO,CO,如图所示:
根据题意得:OD=$\frac{1}{2}$AO,
∴∠OAD=30°,
∴∠AOD=60°,
∴∠AOB=2∠AOD=120°,
同理∠BOC=120°,
∴∠AOC=120°,
∴阴影部分的面积=S扇形AOC=$\frac{1}{3}$×⊙O面积,
故答案为:$\frac{1}{3}$.
点评 本题考查了翻折变换的性质、扇形面积的计算、阴影面积的计算方法;把阴影部分的面积转化为扇形的面积是解决问题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
12.下列四个不等式:①-$\frac{2}{3}$<-0.67;②-$\frac{1}{4}$>-0.24;③-$\frac{5}{6}$>-$\frac{4}{5}$;④-$\frac{3}{11}$<$-\frac{1}{4}$.其中正确的是( )
| A. | ②④ | B. | ①③ | C. | ②③ | D. | ④ |
13.已知关于x的不等式组$\left\{\begin{array}{l}{x≥a-2014}\\{x≤2014-a}\end{array}\right.$无解,化简|a-2013|-|2014-a|的值是( )
| A. | 1 | B. | -1 | C. | 2a-1 | D. | -4027 |
10.设a是方程x2+2x-2=0的一个实数根,则2a2+4a+2016的值为( )
| A. | 2016 | B. | 2018 | C. | 2020 | D. | 2021 |
14.2015年,我市共接待参观旅游游客518 000人,这个数可用科学记数法表示为( )
| A. | 0.518×104 | B. | 5.18×105 | C. | 51.8×106 | D. | 518×103 |
12.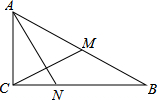 如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )
如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )
 如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )
如图,Rt△ABC中,∠ACB=90°,CM为AB边上的中线,AN⊥CM,交BC于点N,若CM=3,AN=4,则tan∠CAN的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
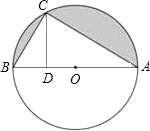 如图,AB是⊙O的直径,C是⊙O上一点,CD⊥AB于D,且AB=8,DB=2.
如图,AB是⊙O的直径,C是⊙O上一点,CD⊥AB于D,且AB=8,DB=2.