题目内容
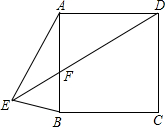 如图,E为正方形ABCD外一点,连接AE,BE,若AE=AB,∠ABE=75°,连接DE交AB于点F,判断△AEF的形状,并说明理由.
如图,E为正方形ABCD外一点,连接AE,BE,若AE=AB,∠ABE=75°,连接DE交AB于点F,判断△AEF的形状,并说明理由.考点:正方形的性质,等腰三角形的判定与性质
专题:
分析:根据等腰三角形两底角相等求出∠BAE,然后求出∠DAE,再根据正方形的性质可得AD=AB=AE,然后利用等腰三角形两底角相等求出∠AEF,根据角的度数求出∠AEF=∠BAE,从而判断出△AEF是等腰三角形.
解答:解:∵AE=AB,∠ABE=75°,
∴∠BAE=180°-75°×2=30°,
∵四边形ABCD是正方形,
∴∠BAD=90°,AD=AB=AE,
∴∠DAE=90°+30°=120°,
∴∠AEF=
(180°-120°)=30°,
∴∠AEF=∠BAE,
∴△AEF是等腰三角形.
∴∠BAE=180°-75°×2=30°,
∵四边形ABCD是正方形,
∴∠BAD=90°,AD=AB=AE,
∴∠DAE=90°+30°=120°,
∴∠AEF=
| 1 |
| 2 |
∴∠AEF=∠BAE,
∴△AEF是等腰三角形.
点评:本题考查了正方形的性质,等腰三角形的判定与性质,熟记性质并根据角的度数得到相等的角是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,B、C为线段AB上的两点,且AB=
如图,B、C为线段AB上的两点,且AB= 如图,已知,如图,BCE,AFE是直线,AD∥BC,∠1=∠2,∠3=∠4,求证:AB∥CD.
如图,已知,如图,BCE,AFE是直线,AD∥BC,∠1=∠2,∠3=∠4,求证:AB∥CD.
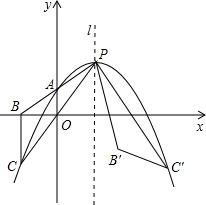 如图,抛物线y=a(x-m)2+2m-2(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m-1).连接并延长PA、PO,与x轴、抛物线分别相交于点B、C,连接BC.点C关于直线l的对称点为C′,连接PC′,即有PC′=PC.将△PBC绕点P逆时针旋转,使点C与点C′重合,得到△PB′C′.
如图,抛物线y=a(x-m)2+2m-2(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m-1).连接并延长PA、PO,与x轴、抛物线分别相交于点B、C,连接BC.点C关于直线l的对称点为C′,连接PC′,即有PC′=PC.将△PBC绕点P逆时针旋转,使点C与点C′重合,得到△PB′C′. 如图,AB是⊙O的直径,弦CD⊥AB,已知
如图,AB是⊙O的直径,弦CD⊥AB,已知