题目内容
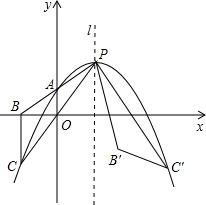 如图,抛物线y=a(x-m)2+2m-2(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m-1).连接并延长PA、PO,与x轴、抛物线分别相交于点B、C,连接BC.点C关于直线l的对称点为C′,连接PC′,即有PC′=PC.将△PBC绕点P逆时针旋转,使点C与点C′重合,得到△PB′C′.
如图,抛物线y=a(x-m)2+2m-2(其中m>1)与其对称轴l相交于点P,与y轴相交于点A(0,m-1).连接并延长PA、PO,与x轴、抛物线分别相交于点B、C,连接BC.点C关于直线l的对称点为C′,连接PC′,即有PC′=PC.将△PBC绕点P逆时针旋转,使点C与点C′重合,得到△PB′C′.(1)该抛物线的解析式为
(2)求证:BC∥y轴;
(3)若点B′恰好落在线段BC′上,求此时m的值.
考点:二次函数综合题,解分式方程,待定系数法求一次函数解析式,待定系数法求二次函数解析式,平行线的判定与性质,三角形内角和定理,等腰三角形的性质,旋转的性质,相似三角形的判定与性质
专题:压轴题
分析:(1)只需将A点坐标(0,m-1)代入y=a(x-m)2+2m-2,即可求出a值,从而得到抛物线的解析式.
(2)由点A、P的坐标可求出直线AP的解析式,从而求出点B的横坐标为-m;由点P的坐标可求出直线OP的解析式,从而求出直线OP与抛物线的交点C的横坐标为-m.由于点B、C的横坐标相同,故BC∥y轴.
(3)利用三角形的内角和定理、图形旋转的性质等知识,结合条件可以证到∠POD=∠BAO,从而可以证到△BAO∽△POD,进而得到
=
,由BO=m,PD=2m-2,AO=m-1,OD=m,可得:
=
,通过解方程就可解决问题.
(2)由点A、P的坐标可求出直线AP的解析式,从而求出点B的横坐标为-m;由点P的坐标可求出直线OP的解析式,从而求出直线OP与抛物线的交点C的横坐标为-m.由于点B、C的横坐标相同,故BC∥y轴.
(3)利用三角形的内角和定理、图形旋转的性质等知识,结合条件可以证到∠POD=∠BAO,从而可以证到△BAO∽△POD,进而得到
| BO |
| PD |
| AO |
| OD |
| m |
| 2m-2 |
| m-1 |
| m |
解答:(1)解:∵A(0,m-1)在抛物线y=a(x-m)2+2m-2上,
∴a(0-m)2+2m-2=m-1.
∴a=
.
∴抛物线的解析式为y=
(x-m)2+2m-2.
(2)证明:如图1,
设直线PA的解析式为y=kx+b,
∵点P(m,2m-2),点A(0,m-1).
∴
.
解得:
.
∴直线PA的解析式是y=
x+m-1.
当y=0时,
x+m-1=0.
∵m>1,
∴x=-m.
∴点B的横坐标是-m.
设直线OP的解析式为y=k′x,
∵点P的坐标为(m,2m-2),
∴k′m=2m-2.
∴k′=
.
∴直线OP的解析式是y=
x.
联立
解得:
或
.
∵点C在第三象限,且m>1,
∴点C的横坐标是-m.
∴BC∥y轴.
(3)解:若点B′恰好落在线段BC′上,
设对称轴l与x轴的交点为D,连接CC′,如图2,
则有∠PB′C′+∠PB′B=180°.
∵△PB′C′是由△PBC绕点P逆时针旋转所得,
∴∠PBC=∠PB′C′,PB=PB′,∠BPB′=∠CPC′.
∴∠PBC+∠PB'B=180°.
∵BC∥AO,
∴∠ABC+∠BAO=180°.
∴∠PB′B=∠BAO.
∵PB=PB′,PC=PC′,
∴∠PB′B=∠PBB′=
,
∴∠PCC′=∠PC′C=
.
∴∠PB′B=∠PCC′.
∴∠BAO=∠PCC′.
∵点C关于直线l的对称点为C′,
∴CC′⊥l.
∵OD⊥l,
∴OD∥CC′.
∴∠POD=∠PCC′.
∴∠POD=∠BAO.
∵∠AOB=∠ODP=90°,∠POD=∠BAO,
∴△BAO∽△POD.
∴
=
.
∵BO=m,PD=2m-2,AO=m-1,OD=m,
∴
=
.
解得:
∴m1=2+
,m2=2-
.
经检验:m1=2+
,m2=2-
都是分式方程的解.
∵m>1,
∴m=2+
.
∴若点B′恰好落在线段BC′上,此时m的值为2+
.
∴a(0-m)2+2m-2=m-1.
∴a=
| 1-m |
| m2 |
∴抛物线的解析式为y=
| 1-m |
| m2 |
(2)证明:如图1,
设直线PA的解析式为y=kx+b,
∵点P(m,2m-2),点A(0,m-1).

∴
|
解得:
|
∴直线PA的解析式是y=
| m-1 |
| m |
当y=0时,
| m-1 |
| m |
∵m>1,
∴x=-m.
∴点B的横坐标是-m.
设直线OP的解析式为y=k′x,
∵点P的坐标为(m,2m-2),
∴k′m=2m-2.
∴k′=
| 2m-2 |
| m |
∴直线OP的解析式是y=
| 2m-2 |
| m |
联立
|
解得:
|
|
∵点C在第三象限,且m>1,
∴点C的横坐标是-m.
∴BC∥y轴.
(3)解:若点B′恰好落在线段BC′上,
设对称轴l与x轴的交点为D,连接CC′,如图2,

则有∠PB′C′+∠PB′B=180°.
∵△PB′C′是由△PBC绕点P逆时针旋转所得,
∴∠PBC=∠PB′C′,PB=PB′,∠BPB′=∠CPC′.
∴∠PBC+∠PB'B=180°.
∵BC∥AO,
∴∠ABC+∠BAO=180°.
∴∠PB′B=∠BAO.
∵PB=PB′,PC=PC′,
∴∠PB′B=∠PBB′=
| 180°-∠BPB′ |
| 2 |
∴∠PCC′=∠PC′C=
| 180°-∠CPC′ |
| 2 |
∴∠PB′B=∠PCC′.
∴∠BAO=∠PCC′.
∵点C关于直线l的对称点为C′,
∴CC′⊥l.
∵OD⊥l,
∴OD∥CC′.
∴∠POD=∠PCC′.
∴∠POD=∠BAO.
∵∠AOB=∠ODP=90°,∠POD=∠BAO,
∴△BAO∽△POD.
∴
| BO |
| PD |
| AO |
| OD |
∵BO=m,PD=2m-2,AO=m-1,OD=m,
∴
| m |
| 2m-2 |
| m-1 |
| m |
解得:
∴m1=2+
| 2 |
| 2 |
经检验:m1=2+
| 2 |
| 2 |
∵m>1,
∴m=2+
| 2 |
∴若点B′恰好落在线段BC′上,此时m的值为2+
| 2 |
点评:本题考查了用待定系数法求二次函数及一次函数的解析式、相似三角形判定与性质、平行线的判定与性质、等腰三角形的性质、解分式方程、三角形的内角和定理、旋转的性质、抛物线与直线的交点等知识,综合性比较强,有一定的难度.而证明∠POD=∠BAO,进而证到△BAO∽△POD是解决第3小题的关键.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
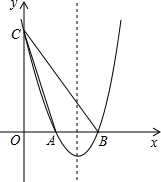 如图,已知二次函数y=a(x2-6x+8)(a>0)的图象与x轴交于点A、B两点,与y轴交于点C.
如图,已知二次函数y=a(x2-6x+8)(a>0)的图象与x轴交于点A、B两点,与y轴交于点C.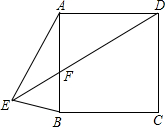 如图,E为正方形ABCD外一点,连接AE,BE,若AE=AB,∠ABE=75°,连接DE交AB于点F,判断△AEF的形状,并说明理由.
如图,E为正方形ABCD外一点,连接AE,BE,若AE=AB,∠ABE=75°,连接DE交AB于点F,判断△AEF的形状,并说明理由.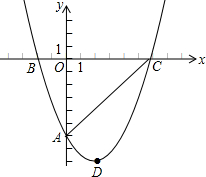 如图,经过点A(0,-6)的抛物线y=
如图,经过点A(0,-6)的抛物线y= 如图,已知抛物线
如图,已知抛物线
