题目内容
17.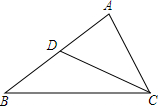 如图,在△ABC中,点D在边AB上,且满足∠ACD=∠ABC.若AC=6cm,AD=4cm,CD=5cm,求DB、BC的长.
如图,在△ABC中,点D在边AB上,且满足∠ACD=∠ABC.若AC=6cm,AD=4cm,CD=5cm,求DB、BC的长.
分析 根据∠ACD=∠ABC,∠A是公共角,得出△ACD∽△ABC,再利用相似三角形的性质进而得出AB,BC的长,然后根据线段的和差求出BD即可.
解答 解:在△ACD和△ABC中,
∵∠ACD=∠ABC,∠A是公共角,
∴△ACD∽△ABC.
∴$\frac{AD}{AC}=\frac{AC}{AB}=\frac{CD}{BC}$
∵AC=6cm,AD=4cm,CD=5cm,
∴AB=9,BC=$\frac{15}{2}$,
∴DB=AB-AD=3.
点评 此题主要考查了相似三角形的判定以及相似三角形的性质,根据已知得出AB的长是解题关键.

练习册系列答案
相关题目
7.在△ABC中,点D与点E分别在边AB、AC上,下列比例式能判断DE∥BC的是( )
| A. | DE:BC=AD:BD | B. | DE:BC=AB:AD | C. | AD:AE=AC:AB | D. | DB:EC=AB:AC |
 如图,将n张长为a cm的纸片一张一张地贴成一个长纸条,每两张纸片重合部分的长度为bcm,试估计贴成的纸条的长度并计算.
如图,将n张长为a cm的纸片一张一张地贴成一个长纸条,每两张纸片重合部分的长度为bcm,试估计贴成的纸条的长度并计算.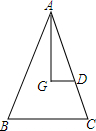 如图,G是△ABC重心,GD∥BC交AC于D,则S△ADG:S△ABC=$\frac{2}{9}$.
如图,G是△ABC重心,GD∥BC交AC于D,则S△ADG:S△ABC=$\frac{2}{9}$. 如图:已知P是半径为5cm的⊙O内一点.解答下列问题:
如图:已知P是半径为5cm的⊙O内一点.解答下列问题: 如图,AC⊥BC,AD⊥CD,∠ACD=∠B,且AB=6,AC=5,求AD的长.
如图,AC⊥BC,AD⊥CD,∠ACD=∠B,且AB=6,AC=5,求AD的长.