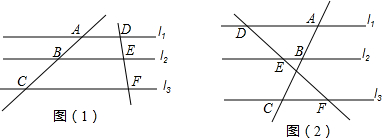题目内容
7.在△ABC中,点D与点E分别在边AB、AC上,下列比例式能判断DE∥BC的是( )| A. | DE:BC=AD:BD | B. | DE:BC=AB:AD | C. | AD:AE=AC:AB | D. | DB:EC=AB:AC |
分析 根据如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边,则当$\frac{AD}{AB}$=$\frac{AE}{AC}$或$\frac{AD}{DB}$=$\frac{AE}{EC}$时,DE∥BC,利用比例性质可判断D正确.
解答  解:如图,
解:如图,
当$\frac{AD}{AB}$=$\frac{AE}{AC}$或$\frac{AD}{DB}$=$\frac{AE}{EC}$时,DE∥BC.
所以$\frac{DB}{EC}$=$\frac{AB}{AC}$时,DE∥BC.
故选D.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例;如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.也考查了比例的性质.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
18.点A(-1,y1),B(-4,y2)在反比例函数$y=-\frac{4}{x}$的图象上,则y1,y2的大小关系是( )
| A. | y1>y2 | B. | y1<y2 | C. | y1=y2 | D. | 不能确定 |
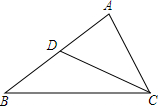 如图,在△ABC中,点D在边AB上,且满足∠ACD=∠ABC.若AC=6cm,AD=4cm,CD=5cm,求DB、BC的长.
如图,在△ABC中,点D在边AB上,且满足∠ACD=∠ABC.若AC=6cm,AD=4cm,CD=5cm,求DB、BC的长.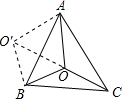 如图,等边△ABC内有一点O,且OA=10,OB=6,OC=8,求∠BOC的度数.(提示:将△AOC顺时针旋转60°后,AC与AB重合,连接OO′)
如图,等边△ABC内有一点O,且OA=10,OB=6,OC=8,求∠BOC的度数.(提示:将△AOC顺时针旋转60°后,AC与AB重合,连接OO′) 已知线段PQ,在PQ上求作一点D,使PD:DQ=2:1.
已知线段PQ,在PQ上求作一点D,使PD:DQ=2:1. 如图△ABC中,G为重心,若AG=2,则AD=3.
如图△ABC中,G为重心,若AG=2,则AD=3.