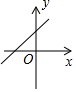题目内容
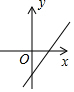
20.已知一次函数y=$-\frac{1}{2}$x+1,它的图象与x轴交于点A,与y轴交于点B.(1)直接写出点A和点B的坐标.
(2)画出该函数的图象.
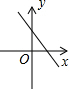
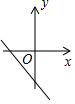
(3)画出该函数向下平移3个单位后得到的函数图象.
(4)写出(3)中函数的解析式.
分析 (1)将y=0代入y=-$\frac{1}{2}$x+1,求出x的值,得到点A的坐标,将x=0代入y=-$\frac{1}{2}$x+1,求出y的值,得到点B的坐标;
(2)根据一次函数的性质,过A,B两点画直线即可;
(3)结合(2)中的图沿y轴向下平移3个单位画出直线即可;
(4)先根据直线平移的规律,将y=-$\frac{1}{2}$x+1向下平移三个单位后得到y=-$\frac{1}{2}$x-2.
解答 解:(1)将y=0代入y=-$\frac{1}{2}$x+1,
得-$\frac{1}{2}$x+1=0,
解得x=2,
则点A的坐标为(2,0).
将x=0代入y=-$\frac{1}{2}$x+1,
得y=-$\frac{1}{2}$×0+1=1,
则点B的坐标为(0,1).
故答案为A(2,0),B(0,1);
(2)如下图: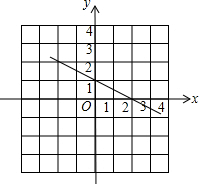
(3)将y=-$\frac{1}{2}$x+1向下平移3个单位后得到的图象如图.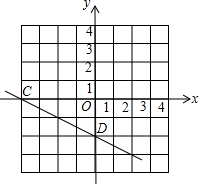
(4)将y=-$\frac{1}{2}$x+1向下平移三个单位后得到y=-$\frac{1}{2}$x-2.
点评 本题考查了一次函数图象上点的坐标特征,一次函数的图象与性质,一次函数图象与几何变换,都是基础知识,需熟练掌握.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目
8.下列各数中无理数有( )
3.414.-$\frac{22}{7}$,$\root{3}{-27}$,-$\sqrt{2}$,π,0.42$\stackrel{••}{17}$,0.2020020002…
3.414.-$\frac{22}{7}$,$\root{3}{-27}$,-$\sqrt{2}$,π,0.42$\stackrel{••}{17}$,0.2020020002…
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
15.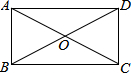 如图,矩形的两条对角线的一个交角为60°,AC+BD=20cm,则AB的长为( )
如图,矩形的两条对角线的一个交角为60°,AC+BD=20cm,则AB的长为( )
 如图,矩形的两条对角线的一个交角为60°,AC+BD=20cm,则AB的长为( )
如图,矩形的两条对角线的一个交角为60°,AC+BD=20cm,则AB的长为( )| A. | 10cm | B. | 8cm | C. | 6cm | D. | 5cm |
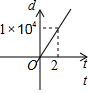
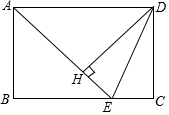 如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接DE,下列结论:①∠AED=∠CED;②△AED为等腰三角形;③EH=CE;④图中有3个等腰三角形.结论正确的个数为( )
如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接DE,下列结论:①∠AED=∠CED;②△AED为等腰三角形;③EH=CE;④图中有3个等腰三角形.结论正确的个数为( )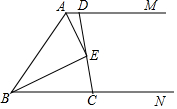 如图,AM∥BN,∠MAB和∠NBA的平分线交于E点.求:
如图,AM∥BN,∠MAB和∠NBA的平分线交于E点.求: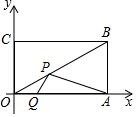 已知在平面直角坐标系中,矩形OABC的顶点O为坐标原点,顶点A、B的坐标分别为(20,0),(20,10).P、Q分别为线段OB、OA上的动点,当PQ+PA最小时,点P的坐标为(12,6).
已知在平面直角坐标系中,矩形OABC的顶点O为坐标原点,顶点A、B的坐标分别为(20,0),(20,10).P、Q分别为线段OB、OA上的动点,当PQ+PA最小时,点P的坐标为(12,6).