题目内容
5.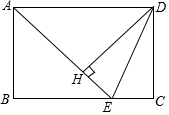 如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接DE,下列结论:①∠AED=∠CED;②△AED为等腰三角形;③EH=CE;④图中有3个等腰三角形.结论正确的个数为( )
如图,在矩形ABCD中,AD=$\sqrt{2}$AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接DE,下列结论:①∠AED=∠CED;②△AED为等腰三角形;③EH=CE;④图中有3个等腰三角形.结论正确的个数为( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 先证明△ABE和△ADH等腰直角三角形,得出AD=AE,AB=AH=DH=DC,得出∠ADE=∠AED,即可得出①②正确;证出∠EDH=∠EDC,由角平分线的性质得出③正确;图中有3个等腰三角形,得出④正确即可.
解答 解:∵四边形ABCD是矩形,
∴∠BAD=∠ABC=∠C=∠ADC=90°,AB=DC,AD∥BC,
∴∠ADE=∠CED,
∵∠BAD的平分线交BC于点E,
∴∠BAE=∠DAH=45°,
∴△ABE和△ADH是等腰直角三角形,
∴AE=$\sqrt{2}$AB,AD=$\sqrt{2}$AH,
∵AD=$\sqrt{2}$AB=$\sqrt{2}$AH,
∴AD=AE,AB=AH=DH=DC,
∴∠ADE=∠AED,
∴∠AED=∠CED,故①②正确;
∵DH⊥AE,DC⊥CE,∠AED=∠CED,
∴∠EDH=∠EDC,
∴EH=CE,故③正确;
∵△ABE和△ADH是等腰直角三角形,△AED为等腰三角形,
∴图中有3个等腰三角形,故④正确;
故选:D.
点评 本题考查了全等三角形的判定与性质、矩形的性质、勾股定理、等腰三角形的判定、角平分线的性质以及等腰直角三角形的判定与性质;熟练掌握矩形的性质和等腰直角三角形的判定与性质是解决问题的关键.

练习册系列答案
相关题目
14.能使式子$\sqrt{2-x}$+$\sqrt{x-1}$成立的x的取值范围是( )
| A. | x≥1 | B. | x≥2 | C. | 1≤x≤2 | D. | x≤2 |
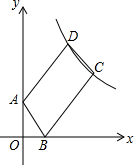 如图,A点坐标为(0,2),B点坐标为(1,0),点C是双曲线y=$\frac{k}{x}$(x>0)的上,将AB沿BC方向从B平移到C,点A的对应点为D,恰有AB=$\frac{1}{2}$BC,且点D也在双曲线上,则k的值等于12.
如图,A点坐标为(0,2),B点坐标为(1,0),点C是双曲线y=$\frac{k}{x}$(x>0)的上,将AB沿BC方向从B平移到C,点A的对应点为D,恰有AB=$\frac{1}{2}$BC,且点D也在双曲线上,则k的值等于12.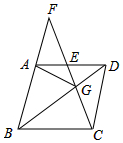 如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.
如图,在菱形ABCD中,G是BD上一点,连接CG并延长交BA的延长线于点F,交AD于点E.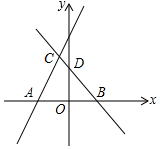 如图,直线y=2x+m(m>0)与x轴交于点A,直线y=-x+n(n>0)与x轴、y轴分别交于B、D,并与直线y=2x+m相交于点C,若AB=4,四边形CAOD的面积为$\frac{10}{3}$,求m、n的值.
如图,直线y=2x+m(m>0)与x轴交于点A,直线y=-x+n(n>0)与x轴、y轴分别交于B、D,并与直线y=2x+m相交于点C,若AB=4,四边形CAOD的面积为$\frac{10}{3}$,求m、n的值.