题目内容

8．如图，函数y1=kx（k＞0）和y2=ax+4（a＜0）的图象相交于点A（m，3），坐标原点为O，AB⊥x轴于点B，△AOB的面积为3，则满足y1＜y2的实数x的取值范围是（　　）
A．x＞2B．x＜2C．x＞3D．x＜3

分析 先根据三角形的面积公式得出m的值，再利用一次函数与不等式的关系解答．

解答 解：因为△AOB的面积为3，函数y1=kx（k＞0）和y2=ax+4（a＜0）的图象相交于点A（m，3），
可得：$\frac{1}{2}×3m=3$，
解得：m=2，
所以满足y1＜y2的实数x的取值范围是x＜2，
故选B

点评 此题考查一次函数与不等式的关系，关键是根据三角形的面积公式得出m的值．

练习册系列答案
相关题目
18．已知点P（m，n）在第四象限，那么点Q（n-1，-m）在（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
19．如图，AB为⊙O的直径，PD切⊙O于点C，交BA的延长线于点D，且CD=CO，则∠PCB等于（　　）
A．67.5°B．60°C．45°D．30°
16．已知不等式组$\left\{\begin{array}{l}{\frac{3x-4}{2}≥1}\\{x≥a}\end{array}\right.$的解集为x≥2，则（　　）
A．a≤2B．a=2C．a＜2D．a≥2
3．如果下列各组数是三角形的三边长，那么不能组成直角三角形的一组数是（　　）
A．1，$\sqrt{3}$，2B．2，3，4C．5，13，12D．$\frac{3}{5}$，$\frac{4}{5}$，1
13．如图①点D、E分别是AB、AC的中点．
（1）△ADE的面积与△ABC的面积存在的数量关系是S△ADE=$\frac{1}{4}$S△ABC．
（2）连接BE，试说明（1）的结论的正确性．
（3）请你用一句话来总结下第一个结论：三角形的中位线把三角形分成的三角形与原三角形的面积比是1：4
（4）请直接应用上面的结论，解决下面的问题：
如图②，已知点D，E，F和点G，H，M分别是△ABC边AB和AC上的点，且AD=DE=EF=FB，AG=GH=HM=MC，若四边形DEHG的面积是9cm2，求△ABC的面积？（直接写出结果，不用说明）．
20．已知直角三角形的两直角边长分别是5和12，则此三角形的斜边长为（　　）
A．10B．13C．15D．17
17．如图①，在平面直角坐标系中，抛物线y=ax2+bx+3交x轴于A（-1，0）和B（5，0）两点，交y轴于点C，点D是线段OB上一动点，连接CD，将线段CD绕点D顺时针旋转90°得到线段DE，过点E作直线l⊥x轴于H，过点C作CF⊥l于点F．
（1）求抛物线解析式；
（2）如图②，当点F恰好在抛物线上时，求线段OD的长；
（3）在（2）的条件下：试探究在直线l上，是否存在点G，使∠EDG=45°．若存在，请直接写出点G的坐标；若不存在，请说明理由．
18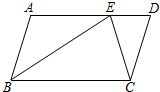．如图，在?ABCD中，AB=6，BC=10，E为AD上一点，且BE=BC，CE=CD，则DE等于（　　）
A．5B．4C．3.6D．3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网