题目内容
19．
如图，AB为⊙O的直径，PD切⊙O于点C，交BA的延长线于点D，且CD=CO，则∠PCB等于（ ）| A． | 67.5° | B． | 60° | C． | 45° | D． | 30° |
分析 由PD切⊙O于点C，得到∠DCO=∠PCO=90°，根据等腰直角三角形的性质得到∠COD=45°，根据外角的性质得到∠ODB=22.5°，即可得到结论．
解答 解：∵PD切⊙O于点C，
∴∠DCO=∠PCO=90°，
∵CD=CO，
∴∠COD=45°，
∵∠COD=∠B+∠OCB，
∴∠ODB=22.5°，
∴∠PCB=67.5°，
故选A．
点评 本题考查切线的性质、等腰直角三角形的性质、圆的有关性质、勾股定理等知识，解题的关键是熟练掌握这些知识的应用，属于基础题，中考常考题型．
练习册系列答案
相关题目
9．函数y=$\frac{x}{3-x}$的自变量取值范围是（ ）
| A． | x≠3 | B． | x≠0 | C． | x≠3且x≠0 | D． | x＜3 |
如图，已知直线y=-x+3与x轴、y轴分别交于A，B两点，抛物线y=-x2+bx+c经过A，B两点，点P在线段OA上，从点O出发，向点A以1个单位/秒的速度匀速运动；同时，点Q在线段AB上，从点A出发，向点B以$\sqrt{2}$个单位/秒的速度匀速运动，连接PQ，设运动时间为t秒．
7．
如图，直线l1：y=x-4与直线l2：y=-$\frac{4}{3}$x+3相交于点（3，-1），则方程组$\left\{\begin{array}{l}{\frac{x}{2}-\frac{y}{2}=2}\\{x+\frac{3y}{4}=\frac{9}{4}}\end{array}\right.$的解是（ ）
如图，直线l1：y=x-4与直线l2：y=-$\frac{4}{3}$x+3相交于点（3，-1），则方程组$\left\{\begin{array}{l}{\frac{x}{2}-\frac{y}{2}=2}\\{x+\frac{3y}{4}=\frac{9}{4}}\end{array}\right.$的解是（ ）| A． | $\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{x=-1}\\{y=-3}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ |
4．
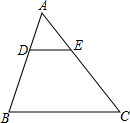如图，在△ABC中，点D、E分别在边AB、AC上，AD：DB=2：3，∠B=∠ADE，则DE：BC等于（ ）
如图，在△ABC中，点D、E分别在边AB、AC上，AD：DB=2：3，∠B=∠ADE，则DE：BC等于（ ）| A． | 1：2 | B． | 1：3 | C． | 2：3 | D． | 2：5 |
11．从下列不等式中选择一个与x+1≥2组成不等式组，使该不等式组的解集为x≥1，那么这个不等式可以是（ ）
| A． | x＞-1 | B． | x＞2 | C． | x＜-1 | D． | x＜2 |
8．
如图，函数y1=kx（k＞0）和y2=ax+4（a＜0）的图象相交于点A（m，3），坐标原点为O，AB⊥x轴于点B，△AOB的面积为3，则满足y1＜y2的实数x的取值范围是（ ）
如图，函数y1=kx（k＞0）和y2=ax+4（a＜0）的图象相交于点A（m，3），坐标原点为O，AB⊥x轴于点B，△AOB的面积为3，则满足y1＜y2的实数x的取值范围是（ ）| A． | x＞2 | B． | x＜2 | C． | x＞3 | D． | x＜3 |
9．若点P（2014，a）、Q（2015，b）都在函数y=$\frac{2016}{x}$的图象上，则下列结论中正确的是（ ）
| A． | a＞b | B． | a=b | ||
| C． | a＜b | D． | a、b的大小关系无法确定 |