题目内容
18.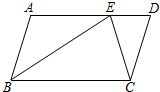 如图,在?ABCD中,AB=6,BC=10,E为AD上一点,且BE=BC,CE=CD,则DE等于( )
如图,在?ABCD中,AB=6,BC=10,E为AD上一点,且BE=BC,CE=CD,则DE等于( )| A. | 5 | B. | 4 | C. | 3.6 | D. | 3 |
分析 先根据平行四边形的性质得出∠2=∠3,再根据BE=BC,CE=CD,∠1=∠2,∠3=∠D,进而得出∠1=∠2=∠3=∠D,故可得出△BCE∽△CDE,再根据相似三角形的对应边成比例即可得出结论.
解答  解:如图所示:
解:如图所示:
∵四边形ABCD是平行四边形,
∴BC=AD=10,AD∥BC,CD=AB=6,
∴∠2=∠3,
∵BE=BC,CE=CD,
∴BE=BC=10,CE=CD=6,∠1=∠2,∠3=∠D,
∴∠1=∠2=∠3=∠D,
∴△BCE∽△CDE,
∴$\frac{BC}{CD}=\frac{CE}{DE}$,即$\frac{10}{6}=\frac{6}{DE}$,
解得:DE=3.6.
故选:C.
点评 本题考查的是相似三角形的判定与性质及平行四边形的性质,根据题意得出△BCE∽△CDE是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8. 如图,函数y1=kx(k>0)和y2=ax+4(a<0)的图象相交于点A(m,3),坐标原点为O,AB⊥x轴于点B,△AOB的面积为3,则满足y1<y2的实数x的取值范围是( )
如图,函数y1=kx(k>0)和y2=ax+4(a<0)的图象相交于点A(m,3),坐标原点为O,AB⊥x轴于点B,△AOB的面积为3,则满足y1<y2的实数x的取值范围是( )
 如图,函数y1=kx(k>0)和y2=ax+4(a<0)的图象相交于点A(m,3),坐标原点为O,AB⊥x轴于点B,△AOB的面积为3,则满足y1<y2的实数x的取值范围是( )
如图,函数y1=kx(k>0)和y2=ax+4(a<0)的图象相交于点A(m,3),坐标原点为O,AB⊥x轴于点B,△AOB的面积为3,则满足y1<y2的实数x的取值范围是( )| A. | x>2 | B. | x<2 | C. | x>3 | D. | x<3 |
9.若点P(2014,a)、Q(2015,b)都在函数y=$\frac{2016}{x}$的图象上,则下列结论中正确的是( )
| A. | a>b | B. | a=b | ||
| C. | a<b | D. | a、b的大小关系无法确定 |
6.若m>n,则下列各式正确的是( )
| A. | m+4<n+4 | B. | 6m<6n | C. | -5m<-5n | D. | 3m-1<3n-1 |
13. 如图所示的△ABC中,∠ABC=90°,∠ACB=40°,AC∥BD,∠ABD=( )
如图所示的△ABC中,∠ABC=90°,∠ACB=40°,AC∥BD,∠ABD=( )
 如图所示的△ABC中,∠ABC=90°,∠ACB=40°,AC∥BD,∠ABD=( )
如图所示的△ABC中,∠ABC=90°,∠ACB=40°,AC∥BD,∠ABD=( )| A. | 40° | B. | 50° | C. | 140° | D. | 130° |
3.命题:“关于x的一元二次方程x2+bx+1=0,当b<0时,必有实数根”;能说明这个命题是假命题的一个反例可以是( )
| A. | b=-1 | B. | b=-2 | C. | b=-3 | D. | b=-4 |
10.菱形ABCD的边长为4,有一个内角为120°,则较长的对角线的长为( )
| A. | 4$\sqrt{3}$ | B. | 4 | C. | $2\sqrt{3}$ | D. | 2 |
7. 如图,AB∥EF∥CD,EG∥BD,则图中与∠1相等的角共有( )
如图,AB∥EF∥CD,EG∥BD,则图中与∠1相等的角共有( )
 如图,AB∥EF∥CD,EG∥BD,则图中与∠1相等的角共有( )
如图,AB∥EF∥CD,EG∥BD,则图中与∠1相等的角共有( )| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
8.某人沿倾斜角为30°的斜坡前进6米,则他上升的最大高度为( )
| A. | 3米 | B. | 3$\sqrt{3}$米 | C. | $\sqrt{3}$米 | D. | 2$\sqrt{3}$米 |