题目内容
13.如图①点D、E分别是AB、AC的中点.(1)△ADE的面积与△ABC的面积存在的数量关系是S△ADE=$\frac{1}{4}$S△ABC.
(2)连接BE,试说明(1)的结论的正确性.
(3)请你用一句话来总结下第一个结论:三角形的中位线把三角形分成的三角形与原三角形的面积比是1:4
(4)请直接应用上面的结论,解决下面的问题:
如图②,已知点D,E,F和点G,H,M分别是△ABC边AB和AC上的点,且AD=DE=EF=FB,AG=GH=HM=MC,若四边形DEHG的面积是9cm2,求△ABC的面积?(直接写出结果,不用说明).

分析 (1)利用三角形的中线把三角形分成面积相等的两个三角形即可;
(2)利用三角形的中线把三角形分成面积相等的两个三角形即可;
(3)有(1)(2)直接总结出结论;
(4)由前面的结论直接进行计算即可.
解答 解:(1)结论:S△ADE=$\frac{1}{4}$S△ABC,
故答案为:S△ADE=$\frac{1}{4}$S△ABC,
(2)如图①,连接BE,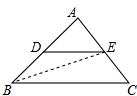
∵点E是AC中点,
∴S△ABE=$\frac{1}{2}$S△ABC,
∵点D是AB中点,
∴S△ADE=$\frac{1}{2}$S△ABE=$\frac{1}{4}$S△ABC,
(3)结论:三角形的中位线把三角形分成的三角形与原三角形的面积比是1:4,
故答案为:三角形的中位线把三角形分成的三角形与原三角形的面积比是1:4;
(4)∵AD=DE,AG=GH
∴由(1)的结论得,S△ADG=$\frac{1}{4}$S△AEH,
∵S△AEH=S△ADG+S四边形DEHG,
∴S△AEH=$\frac{4}{3}$S四边形DEHG=$\frac{4}{3}$×9=12,
∵AD=DE=EF=FB,AG=GH=HM=MC,
∴AE=EB,AH=HC,
∴S△AEH=$\frac{1}{4}$S△ABC,
∴S△ABC=4S△AEH=4×12=48,
∴△ABC的面积为48cm2.
点评 此题是三角形综合题,主要考查了三角形中线的性质,比例的基本性质,解本题的关键是用比例的基本性质进行等式变形.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
3.直线l1:y=x+1与直线l2:y=mx+n的交点P的横坐标为1,则下列说法错误的是( )
| A. | 点P的坐标为(1,2) | |
| B. | 关于x、y的方程组$\left\{\begin{array}{l}{y=x+1}\\{y=mx+n}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$ | |
| C. | 直线l1中,y随x的增大而减小 | |
| D. | 直线y=nx+m也经过点P |
4.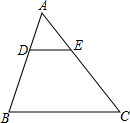 如图,在△ABC中,点D、E分别在边AB、AC上,AD:DB=2:3,∠B=∠ADE,则DE:BC等于( )
如图,在△ABC中,点D、E分别在边AB、AC上,AD:DB=2:3,∠B=∠ADE,则DE:BC等于( )
 如图,在△ABC中,点D、E分别在边AB、AC上,AD:DB=2:3,∠B=∠ADE,则DE:BC等于( )
如图,在△ABC中,点D、E分别在边AB、AC上,AD:DB=2:3,∠B=∠ADE,则DE:BC等于( )| A. | 1:2 | B. | 1:3 | C. | 2:3 | D. | 2:5 |
1.一次函数y=2x+4与x轴交点的坐标为( )
| A. | (0,4) | B. | (4,0) | C. | (-2,0) | D. | (0,-2) |
8. 如图,函数y1=kx(k>0)和y2=ax+4(a<0)的图象相交于点A(m,3),坐标原点为O,AB⊥x轴于点B,△AOB的面积为3,则满足y1<y2的实数x的取值范围是( )
如图,函数y1=kx(k>0)和y2=ax+4(a<0)的图象相交于点A(m,3),坐标原点为O,AB⊥x轴于点B,△AOB的面积为3,则满足y1<y2的实数x的取值范围是( )
 如图,函数y1=kx(k>0)和y2=ax+4(a<0)的图象相交于点A(m,3),坐标原点为O,AB⊥x轴于点B,△AOB的面积为3,则满足y1<y2的实数x的取值范围是( )
如图,函数y1=kx(k>0)和y2=ax+4(a<0)的图象相交于点A(m,3),坐标原点为O,AB⊥x轴于点B,△AOB的面积为3,则满足y1<y2的实数x的取值范围是( )| A. | x>2 | B. | x<2 | C. | x>3 | D. | x<3 |
2.下列命题中:
①同位角相等,两直线平行;
②在△ABC中,a,b,c分别是∠A、∠B、∠C的对边,如果∠C=90°,那么a2+b2=c2;
③菱形是对角线互相垂直的四边形;
④矩形是对角线相等的平行四边形.
它们的逆命题是真命题的有( )
①同位角相等,两直线平行;
②在△ABC中,a,b,c分别是∠A、∠B、∠C的对边,如果∠C=90°,那么a2+b2=c2;
③菱形是对角线互相垂直的四边形;
④矩形是对角线相等的平行四边形.
它们的逆命题是真命题的有( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
3.命题:“关于x的一元二次方程x2+bx+1=0,当b<0时,必有实数根”;能说明这个命题是假命题的一个反例可以是( )
| A. | b=-1 | B. | b=-2 | C. | b=-3 | D. | b=-4 |