题目内容
17.如图①,在平面直角坐标系中,抛物线y=ax2+bx+3交x轴于A(-1,0)和B(5,0)两点,交y轴于点C,点D是线段OB上一动点,连接CD,将线段CD绕点D顺时针旋转90°得到线段DE,过点E作直线l⊥x轴于H,过点C作CF⊥l于点F.(1)求抛物线解析式;
(2)如图②,当点F恰好在抛物线上时,求线段OD的长;
(3)在(2)的条件下:试探究在直线l上,是否存在点G,使∠EDG=45°.若存在,请直接写出点G的坐标;若不存在,请说明理由.

分析 (1)用待定系数法求抛物线解析式即可;
(2)先求出点F(4,3),在判断出△OCD≌△HDE,再做简单的计算即可;
(3)先求出E(4,1),再根据直线之间的关系用待定系数法依次求出,直线CE解析式为y=-$\frac{1}{2}$x+3,直线DG2的解析式为y=-$\frac{1}{2}$x+3,即可.
解答 解:(1)∵抛物线y=ax2+bx+3交x轴于A(-1,0),B(5,0),
∴$\left\{\begin{array}{l}{a-b+3=0}\\{25a+5b+3=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=-\frac{3}{5}}\\{b=\frac{12}{5}}\end{array}\right.$,
∴抛物线y=-$\frac{3}{5}$x2+$\frac{12}{5}$x+3,
(2)∵点F恰好在抛物线上,C(0,3),
∴F的纵坐标为3,
把y=3代入y=-$\frac{3}{5}$x2+$\frac{12}{5}$x+3,得3=-$\frac{3}{5}$x2+$\frac{12}{5}$x+3,
∴x=0,或x=4,
∴F(4,3),
∴OH=4,
∵∠CDE=90°,
∴∠ODC+∠HDC=90°,
∴∠OCD=∠HDE,
在△OCD和△HDE中,
$\left\{\begin{array}{l}{∠OCD=∠HDE}\\{∠COD=DHE}\\{CD=DE}\end{array}\right.$,
∴△OCD≌△HDE,
∴DH=OC=3,
∴OD=4-3=1;
(3)存在,如图,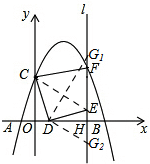
连接CE,
∵CD=DE,∠CDE=90°,
∴∠CED=45°,
过点D作DG1∥CE,过点D作DG2⊥CE,
∴∠EDG1=45°,∠EDG2=45°,
∵EH=OD=1,OH=4,
∴E(4,1),
∵C(0,3),
∴直线CE解析式为y=-$\frac{1}{2}$x+3,
设直线DG2的解析式为y=-$\frac{1}{2}$x+m,
∵D(1,0),
∴0=-$\frac{1}{2}$×1+m,
∴m=$\frac{1}{2}$,
∴直线DG2的解析式为y=-$\frac{1}{2}$x+3,
当x=4时,y=-$\frac{1}{2}$×4×+$\frac{1}{2}$=-$\frac{3}{2}$,
∴G1(4,-$\frac{3}{2}$),
设直线DG1的解析式为y=2x+n,
∵D(1,0),
∴0=2×1+n,
∴n=-2,
∴直线DG1的解析式为y=2x-2.
当x=4时,y=6,
∴G2(4,6).
点评 此题是二次函数综合题,主要考查了用待定系数法求抛物线,直线解析式,三角形全等的判定和性质,解本题的关键是寻找出直线之间的关系来确定直线解析式.

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案 如图,直线l1:y=x-4与直线l2:y=-$\frac{4}{3}$x+3相交于点(3,-1),则方程组$\left\{\begin{array}{l}{\frac{x}{2}-\frac{y}{2}=2}\\{x+\frac{3y}{4}=\frac{9}{4}}\end{array}\right.$的解是( )
如图,直线l1:y=x-4与直线l2:y=-$\frac{4}{3}$x+3相交于点(3,-1),则方程组$\left\{\begin{array}{l}{\frac{x}{2}-\frac{y}{2}=2}\\{x+\frac{3y}{4}=\frac{9}{4}}\end{array}\right.$的解是( )| A. | $\left\{\begin{array}{l}{x=3}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-1}\\{y=3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=-1}\\{y=-3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$ |
 如图,函数y1=kx(k>0)和y2=ax+4(a<0)的图象相交于点A(m,3),坐标原点为O,AB⊥x轴于点B,△AOB的面积为3,则满足y1<y2的实数x的取值范围是( )
如图,函数y1=kx(k>0)和y2=ax+4(a<0)的图象相交于点A(m,3),坐标原点为O,AB⊥x轴于点B,△AOB的面积为3,则满足y1<y2的实数x的取值范围是( )| A. | x>2 | B. | x<2 | C. | x>3 | D. | x<3 |
①同位角相等,两直线平行;
②在△ABC中,a,b,c分别是∠A、∠B、∠C的对边,如果∠C=90°,那么a2+b2=c2;
③菱形是对角线互相垂直的四边形;
④矩形是对角线相等的平行四边形.
它们的逆命题是真命题的有( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
| A. | a>b | B. | a=b | ||
| C. | a<b | D. | a、b的大小关系无法确定 |
| A. | m+4<n+4 | B. | 6m<6n | C. | -5m<-5n | D. | 3m-1<3n-1 |
 如图,AB∥EF∥CD,EG∥BD,则图中与∠1相等的角共有( )
如图,AB∥EF∥CD,EG∥BD,则图中与∠1相等的角共有( )| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |