题目内容
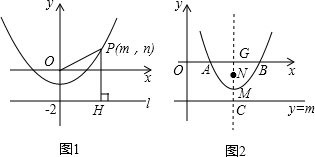
如图1,P(m,n)是抛物线y=
x2-1上任意一点,l是过点(0,-2)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.
【特例探究】
(1)填空,当m=0时,OP= ,PH= ;当m=4时,OP= ,PH= .
【猜想验证】
(2)对任意m,n,猜想OP与PH大小关系,并证明你的猜想.
【拓展应用】
(3)如图2,如果图1中的抛物线y=
x2-1变成y=x2-4x+3,直线l变成y=m(m<-1).已知抛物线y=x2-4x+3的顶点为M,交x轴于A、B两点,且B点坐标为(3,0),N是对称轴上的一点,直线y=m(m<-1)与对称轴于点C,若对于抛物线上每一点都有:该点到直线y=m的距离等于该点到点N的距离.
①用含m的代数式表示MC、MN及GN的长,并写出相应的解答过程;
②求m的值及点N的坐标.
| 1 |
| 4 |
【特例探究】
(1)填空,当m=0时,OP=
【猜想验证】
(2)对任意m,n,猜想OP与PH大小关系,并证明你的猜想.
【拓展应用】
(3)如图2,如果图1中的抛物线y=
| 1 |
| 4 |
①用含m的代数式表示MC、MN及GN的长,并写出相应的解答过程;
②求m的值及点N的坐标.

考点:二次函数综合题
专题:
分析:(1)根据勾股定理,可得OP的长,根据点到直线的距离,可得可得PH的长;
(2)根据图象上的点满足函数解析式,可得点的坐标,根据勾股定理,可得PO的长,根据点到直线的距离,可得PH的长;
(3)①根据该点到直线y=m的距离等于该点到点N的距离,可得CM=MN,根据线段的和差,可得GN的长;
②对于抛物线上每一点都有:该点到直线y=m的距离等于该点到点N的距离,可得方程,根据解方程,可得m的值,再根据线段的和差,可得GN的长.
(2)根据图象上的点满足函数解析式,可得点的坐标,根据勾股定理,可得PO的长,根据点到直线的距离,可得PH的长;
(3)①根据该点到直线y=m的距离等于该点到点N的距离,可得CM=MN,根据线段的和差,可得GN的长;
②对于抛物线上每一点都有:该点到直线y=m的距离等于该点到点N的距离,可得方程,根据解方程,可得m的值,再根据线段的和差,可得GN的长.
解答:解:(1)当m=0时,P(0,-1),OP=1,PH=-1-(-2)=1;
当m=4时,y=3,P(4,3),OP=
=5,PH=3-(-2)=3+2=5,
故答案为:1,1,5,5;
(2)猜想:OP=PH,
证明:PH交x轴与点Q,
∵P在y=
x2-1上,
∴设P(m,
m2-1),PQ=|
x2-1|,OQ=|m|,
∵△OPQ是直角三角形,
∴OP=
=
=
=
m2+1,
PH=yp-(-2)=(
m2-1)-(-2)=
m2+1
OP=PH.
(3)①CM=MN=-m-1,GN=2+m,
理由如下:对于抛物线上每一点都有:该点到直线y=m的距离等于该点到点N的距离,
M(2,-1),即CM=MN=-m-1.
GN=CG-CM-MN=-m-2(-m-1)=2+m.
②点B的坐标是(3,0),BG=1,GN=2+m.
由勾股定理,得BN=
=
,
对于抛物线上每一点都有:该点到直线y=m的距离等于该点到点N的距离,得
即1+(2+m)2=(-m)2.
解得m=-
.
由GN=2+m=2-
=
,即N(2,-
),
∴m=-
,N点的坐标是(2,-
).
当m=4时,y=3,P(4,3),OP=
| 42+32 |
故答案为:1,1,5,5;
(2)猜想:OP=PH,
证明:PH交x轴与点Q,
∵P在y=
| 1 |
| 4 |
∴设P(m,
| 1 |
| 4 |
| 1 |
| 4 |
∵△OPQ是直角三角形,
∴OP=
| PQ2+OQ2 |
(
|
(
|
| 1 |
| 4 |
PH=yp-(-2)=(
| 1 |
| 4 |
| 1 |
| 4 |
OP=PH.
(3)①CM=MN=-m-1,GN=2+m,
理由如下:对于抛物线上每一点都有:该点到直线y=m的距离等于该点到点N的距离,
M(2,-1),即CM=MN=-m-1.
GN=CG-CM-MN=-m-2(-m-1)=2+m.
②点B的坐标是(3,0),BG=1,GN=2+m.
由勾股定理,得BN=
| BG2+GN2 |
| 12+(2+m)2 |
对于抛物线上每一点都有:该点到直线y=m的距离等于该点到点N的距离,得
即1+(2+m)2=(-m)2.
解得m=-
| 5 |
| 4 |
由GN=2+m=2-
| 5 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
∴m=-
| 5 |
| 4 |
| 3 |
| 4 |
点评:本题考查了二次函数综合题,利用了勾股定理,点到直线的距离,线段中点的性质,线段的和差,利用的知识点较多,题目稍有难度.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
 如图,AB∥DE,∠A=120°,C=80°,则∠D的度数为( )
如图,AB∥DE,∠A=120°,C=80°,则∠D的度数为( )| A、130° | B、120° |
| C、160° | D、145° |
 ”图案.
”图案.
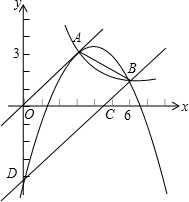 如图,已知正比例函数和反比例函数的图象都经过点A(3,3).
如图,已知正比例函数和反比例函数的图象都经过点A(3,3).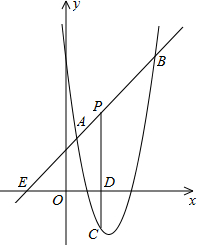 如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(