题目内容
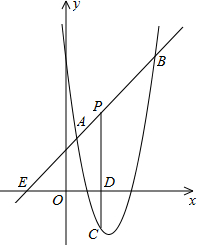 如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(| 1 |
| 2 |
| 5 |
| 2 |
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)将点B坐标代入直线解析式,求出m的值,然后把A、B坐标代入二次函数解析式,求出a、b,即可求得解析式;
(2)设动点P的坐标为(n,n+2),点C的坐标为(n,2n2-8n+6),表示出PC的长度,然后利用配方法求出二次函数的最大值,并求出此时n的值.
(2)设动点P的坐标为(n,n+2),点C的坐标为(n,2n2-8n+6),表示出PC的长度,然后利用配方法求出二次函数的最大值,并求出此时n的值.
解答:解:(1)∵B(4,m)在直线y=x+2上,
∴m=6,即B(4,6),
∵A(
,
)和B(4,6)在抛物线y=ax2+bx+6上,
∴
,
解得:
,
∴抛物线的解析式y=2x2-8x+6;
(2)存在.
设动点P的坐标为(n,n+2),点C的坐标为(n,2n2-8n+6),
∴PC=(n+2)-(2n2-8n+6)=-2n2+9n-4=-2(n-
)2+
,
∵-2<0,
∴开口向下,有最大值,
∴当n=
时,线段PC有最大值
.
∴m=6,即B(4,6),
∵A(
| 1 |
| 2 |
| 5 |
| 2 |
∴
|
解得:
|
∴抛物线的解析式y=2x2-8x+6;
(2)存在.
设动点P的坐标为(n,n+2),点C的坐标为(n,2n2-8n+6),
∴PC=(n+2)-(2n2-8n+6)=-2n2+9n-4=-2(n-
| 9 |
| 4 |
| 49 |
| 8 |
∵-2<0,
∴开口向下,有最大值,
∴当n=
| 9 |
| 4 |
| 49 |
| 8 |
点评:本题考查了二次函数的综合运用,涉及了待定系数法求函数解析式,配方法求最值等知识点,解答本题案的关键是根据解析式设出点P和点C的坐标,列出PC的代数式.

练习册系列答案
相关题目
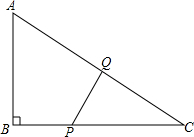 如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米,点P从点B出发,沿BC以1厘米/秒的速度向点C移动,点Q从点C出发,沿折线CAB以2厘米/秒的速度向点B移动.问:
如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米,点P从点B出发,沿BC以1厘米/秒的速度向点C移动,点Q从点C出发,沿折线CAB以2厘米/秒的速度向点B移动.问:
 作出如图立体图形的三视图.
作出如图立体图形的三视图. 如图,小方格都是边长为1的正方形,则以格点为圆心,半径为1和2的两种弧围成的“叶片状”阴影图案的面积为
如图,小方格都是边长为1的正方形,则以格点为圆心,半径为1和2的两种弧围成的“叶片状”阴影图案的面积为