题目内容
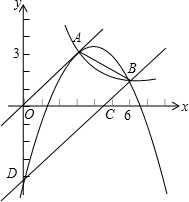 如图,已知正比例函数和反比例函数的图象都经过点A(3,3).
如图,已知正比例函数和反比例函数的图象都经过点A(3,3).(1)求正比例函数和反比例函数的解析式;
(2)把直线OA向下平移后与反比例函数的图象交于点B(6,m),求m的值和这个一次函数的解析式;
(3)第(2)问中的一次函数的图象与x轴、y轴分别交于C、D,求过A、B、D三点的三角形的面积.
(4)在第(3)问的条件下,二次函数的图象上是否存在点E,使四边形OECD的面积S1与四边形OABD的面积S满足:S1=
| 2 |
| 3 |
考点:反比例函数综合题
专题:
分析:(1)利用待定系数法即可求得函数的解析式;
(2)根据直线平移的方法即可求解;
(3)作AM⊥y轴于点M,作BN⊥y轴于点N,根据S四边形ABDM=S梯形ABNM+S△BDN,S△ABD=S四边形ABDM-S△ADM即可求解;
(4)首先求得D的坐标,然后利用待定系数法求得二次函数的解析式,根据S1=S△OCD+S△OCE即可求得S1的值,进而求得S2,根据E(x0,y0)在二次函数的图象上,即可求得x0的值,进而求得E的坐标.
(2)根据直线平移的方法即可求解;
(3)作AM⊥y轴于点M,作BN⊥y轴于点N,根据S四边形ABDM=S梯形ABNM+S△BDN,S△ABD=S四边形ABDM-S△ADM即可求解;
(4)首先求得D的坐标,然后利用待定系数法求得二次函数的解析式,根据S1=S△OCD+S△OCE即可求得S1的值,进而求得S2,根据E(x0,y0)在二次函数的图象上,即可求得x0的值,进而求得E的坐标.
解答:解:(1)设正比例函数的解析式是y=kx,代入(3,3),得:3k=3,解得:k=1,
则正比例函数的解析式是:y=x;
设反比例函数的解析式是y=
,把(3,3)代入解析式得:k1=9,
则反比例函数的解析式是:y=
;
(2)m=
=
,则点B的坐标是(6,
),
∵y=k3x+b的图象是由y=x平移得到,
∴k3=1,即y=x+b,
一次函数的解析式是:y=x-
;
(3)∵y=x-
的图象交y轴于点D,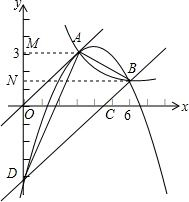
∴D的坐标是(0,-
),
作AM⊥y轴于点M,作BN⊥y轴于点N.
∵A的坐标是(3,3),B的坐标是(6,
),
∴M的坐标是(0,3),N的坐标是(0,
).
∴OM=3,ON=
.
则MD=3+
=
,DN=
+
=6,MN=3-
=
.
则S△ADM=
×3×
=
,S△BDN=
×6×6=18,S梯形ABNM=
(3+6)×
=
.
则S四边形ABDM=S梯形ABNM+S△BDN=
+18=
,
S△ABD=S四边形ABDM-S△ADM=
-
=
=
;
(4)设二次函数的解析式是y=ax2+bx-
,
则
,
解得:
,
则这个二次函数的解析式是:y=-
x2+4x-
;
点C的坐标是(
,0).
则S=
×6-
×6×6-
×3×3=45-18-
-
=
.
假设存在点E(x0,y0),使S1=
S=
×
=
.
∵四边形CDOE的顶点E只能在x轴的上方,
∴y0>0,
∴S1=S△OCD+S△OCE=
×
×
+
y0
=
+
y0,
∴
+
y0=
,
∴y0=
,
∵E(x0,y0)在二次函数的图象上,
∴-
x02+4x0-
=
,
解得:x0=2或6.
当x0=6时,点E(6,
)与点B重合,这时CDOE不是四边形,故x0=6,(舍去).
∴E的坐标是(2,
).
则正比例函数的解析式是:y=x;
设反比例函数的解析式是y=
| k1 |
| x |
则反比例函数的解析式是:y=
| 9 |
| x |
(2)m=
| 9 |
| 6 |
| 3 |
| 2 |
| 3 |
| 2 |
∵y=k3x+b的图象是由y=x平移得到,
∴k3=1,即y=x+b,
一次函数的解析式是:y=x-
| 9 |
| 2 |
(3)∵y=x-
| 9 |
| 2 |

∴D的坐标是(0,-
| 9 |
| 2 |
作AM⊥y轴于点M,作BN⊥y轴于点N.
∵A的坐标是(3,3),B的坐标是(6,
| 3 |
| 2 |
∴M的坐标是(0,3),N的坐标是(0,
| 3 |
| 2 |
∴OM=3,ON=
| 3 |
| 2 |
则MD=3+
| 9 |
| 2 |
| 15 |
| 2 |
| 3 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
则S△ADM=
| 1 |
| 2 |
| 15 |
| 2 |
| 45 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 27 |
| 4 |
则S四边形ABDM=S梯形ABNM+S△BDN=
| 27 |
| 4 |
| 99 |
| 4 |
S△ABD=S四边形ABDM-S△ADM=
| 99 |
| 4 |
| 45 |
| 4 |
| 54 |
| 4 |
| 27 |
| 2 |
(4)设二次函数的解析式是y=ax2+bx-
| 9 |
| 2 |
则
|
解得:
|
则这个二次函数的解析式是:y=-
| 1 |
| 2 |
| 9 |
| 2 |
点C的坐标是(
| 9 |
| 2 |
则S=
| 15 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
| 9 |
| 2 |
| 81 |
| 4 |
假设存在点E(x0,y0),使S1=
| 2 |
| 3 |
| 81 |
| 4 |
| 2 |
| 3 |
| 27 |
| 2 |
∵四边形CDOE的顶点E只能在x轴的上方,
∴y0>0,
∴S1=S△OCD+S△OCE=
| 1 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
=
| 81 |
| 8 |
| 9 |
| 4 |
∴
| 81 |
| 8 |
| 9 |
| 4 |
| 27 |
| 2 |
∴y0=
| 3 |
| 2 |
∵E(x0,y0)在二次函数的图象上,
∴-
| 1 |
| 2 |
| 9 |
| 2 |
| 3 |
| 2 |
解得:x0=2或6.
当x0=6时,点E(6,
| 3 |
| 2 |
∴E的坐标是(2,
| 3 |
| 2 |
点评:本题是一次函数、反比例函数、二次函数的综合应用,待定系数法求函数解析式是基本方法,根据四边形CDOE的面积求得E的纵坐标是解决本题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
正多边形的中心角是36°,那么这个正多边形的边数是( )
| A、10 | B、8 | C、6 | D、5 |
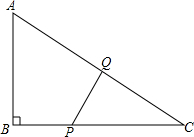 如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米,点P从点B出发,沿BC以1厘米/秒的速度向点C移动,点Q从点C出发,沿折线CAB以2厘米/秒的速度向点B移动.问:
如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米,点P从点B出发,沿BC以1厘米/秒的速度向点C移动,点Q从点C出发,沿折线CAB以2厘米/秒的速度向点B移动.问:
 如图,小方格都是边长为1的正方形,则以格点为圆心,半径为1和2的两种弧围成的“叶片状”阴影图案的面积为
如图,小方格都是边长为1的正方形,则以格点为圆心,半径为1和2的两种弧围成的“叶片状”阴影图案的面积为