题目内容
9.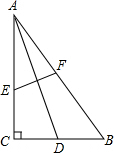 如图,在Rt△ABC中,∠C=90°,AC=BC=2,AD是BC边上的中线,将A点翻折与点D重合,得到折痕EF,求CE:AE的值.
如图,在Rt△ABC中,∠C=90°,AC=BC=2,AD是BC边上的中线,将A点翻折与点D重合,得到折痕EF,求CE:AE的值.
分析 连接ED,设AC=BC=x,CE=y,根据勾股定理列出方程,解方程求出x、y的关系,计算即可.
解答  解:连接ED,
解:连接ED,
设CE=y,
∵AD是BC边上的中线,
∴CD=1,
由翻转变换的性质可知,DE=AE=2-y,
由勾股定理得,(2-y)2=12+y2,
解得,y=$\frac{3}{4}$,
则$\frac{CE}{AE}$=$\frac{3}{5}$.
点评 本题考查的是翻转变换的性质、勾股定理的应用,掌握翻转变换的性质、灵活运用方程思想是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
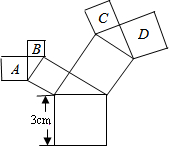 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为3cm,则图中所有正方形的面积之和为27cm2.
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为3cm,则图中所有正方形的面积之和为27cm2. △ABC在平面直角坐标系xOy中的位置如图所示.
△ABC在平面直角坐标系xOy中的位置如图所示.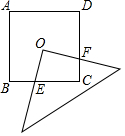 如图,有一个边长为4cm的正方形ABCD,将一块45°的三角板直角顶点与正方形对角线交点O重合,两条直角边分别与BC边交于点E,与CD边交于点F.则四边形OECF的面积是4cm2.
如图,有一个边长为4cm的正方形ABCD,将一块45°的三角板直角顶点与正方形对角线交点O重合,两条直角边分别与BC边交于点E,与CD边交于点F.则四边形OECF的面积是4cm2. 如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论: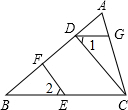 如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上.
如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上.