题目内容
19.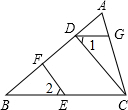 如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上.
如图,在△ABC中,∠1=∠2,点E、F、G分别在BC、AB、AC上.(1)若在△BCD中,BC=5,BD=4,设CD的长为奇数,则CD的取值是3,5,7;
(2)若EF⊥AB,DG∥BC,请判断CD与AB的位置关系,并说明理由.
分析 (1)根据三角形三边关系定理求出CD取值范围,再根据CD的长为奇数即可得出CD的取值;
(2)由平行线的性质和已知条件可证明CD∥EF,可求得∠CDB=90°,可判断CD⊥AB.
解答 解:(1)∵在△BCD中,BC=5,BD=4,
∴1<CD<9,
∵CD的长为奇数,
∴CD的取值是3,5,7.
故答案为3,5,7; (2)CD⊥AB.理由如下:
(2)CD⊥AB.理由如下:
∴DG∥BC,
∴∠1=∠DCB,
∵∠1=∠2,
∴∠2=∠DCB,
∴CD∥EF,
∴∠CDB=∠EFB,
∵EF⊥AB,
∴∠EFB=90°,
∴∠CDB=90°,
∴CD⊥AB.
点评 本题考查了三角形三边关系定理,平行线的性质和判定,掌握定理与性质是解题的关键.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
10.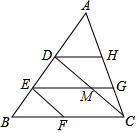 如图,DH∥EG∥BC,DC∥EF,那么与∠DCB相等的角的个数为( )
如图,DH∥EG∥BC,DC∥EF,那么与∠DCB相等的角的个数为( )
 如图,DH∥EG∥BC,DC∥EF,那么与∠DCB相等的角的个数为( )
如图,DH∥EG∥BC,DC∥EF,那么与∠DCB相等的角的个数为( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
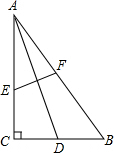 如图,在Rt△ABC中,∠C=90°,AC=BC=2,AD是BC边上的中线,将A点翻折与点D重合,得到折痕EF,求CE:AE的值.
如图,在Rt△ABC中,∠C=90°,AC=BC=2,AD是BC边上的中线,将A点翻折与点D重合,得到折痕EF,求CE:AE的值.



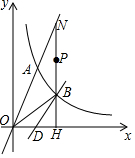 直线y=x-1交x轴于D点,交双曲线y=$\frac{k}{x}$(k>0)于B点,直线y=2x交双曲线y=$\frac{k}{x}$(k>0)于A点.
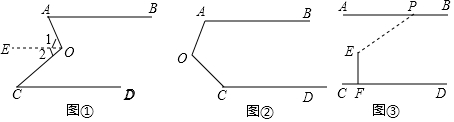
直线y=x-1交x轴于D点,交双曲线y=$\frac{k}{x}$(k>0)于B点,直线y=2x交双曲线y=$\frac{k}{x}$(k>0)于A点.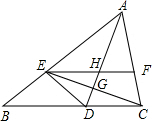 如图,AD是∠BAC平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F,AD与CE交于点G,与EF交于点H.
如图,AD是∠BAC平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F,AD与CE交于点G,与EF交于点H.