题目内容
1.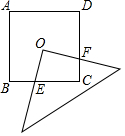 如图,有一个边长为4cm的正方形ABCD,将一块45°的三角板直角顶点与正方形对角线交点O重合,两条直角边分别与BC边交于点E,与CD边交于点F.则四边形OECF的面积是4cm2.
如图,有一个边长为4cm的正方形ABCD,将一块45°的三角板直角顶点与正方形对角线交点O重合,两条直角边分别与BC边交于点E,与CD边交于点F.则四边形OECF的面积是4cm2.
分析 根据正方形的性质得出OA=OB=OC=OD,∠BOC=90°,∠OCF=∠OBE=45°,求出∠BOE=∠COF,根据全等三角形的判定得出△BOE≌△COF,即可求出四边形EOCF的面积=三角形BOC的面积,即可得出答案.
解答 解: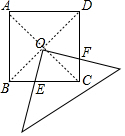
连接AC和BD,则AC、BD都过O,
∵四边形ABCD是正方形,
∴OA=OB=OC=OD,∠BOC=90°,∠OCF=∠OBE=45°,
∴S△BOC=$\frac{1}{4}$S正方形ABCD=4cm×4cm×$\frac{1}{4}$=4cm2,
∵∠EOF=∠BOC=90°,
∴∠BOE=∠COF=90°-∠EOC,
在△BOE和△COF中
$\left\{\begin{array}{l}{∠BOE=∠COF}\\{OB=OC}\\{∠OBE=∠OCF}\end{array}\right.$
∴△BOE≌△COF(ASA),
∴S△BOE=S△COF,
∴S四边形OECF=S△EOC+S△COF=S△EOC+S△BOE=S△BOC=4cm2
故答案为:4.
点评 本题考查了正方形的性质,全等三角形的性质和判定等知识点,本题的解题关键是知道题中重合的部分的面积是不变的,总是等于正方形ABCD面积的$\frac{1}{4}$.

练习册系列答案
相关题目
10.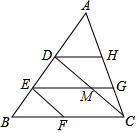 如图,DH∥EG∥BC,DC∥EF,那么与∠DCB相等的角的个数为( )
如图,DH∥EG∥BC,DC∥EF,那么与∠DCB相等的角的个数为( )
 如图,DH∥EG∥BC,DC∥EF,那么与∠DCB相等的角的个数为( )
如图,DH∥EG∥BC,DC∥EF,那么与∠DCB相等的角的个数为( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
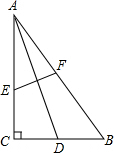 如图,在Rt△ABC中,∠C=90°,AC=BC=2,AD是BC边上的中线,将A点翻折与点D重合,得到折痕EF,求CE:AE的值.
如图,在Rt△ABC中,∠C=90°,AC=BC=2,AD是BC边上的中线,将A点翻折与点D重合,得到折痕EF,求CE:AE的值.
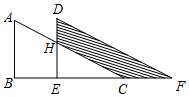 如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着B到点C的方向平移到△DEF的位置,AB=10,EH=7,平移距离是6,则图中阴影部分的面积为30.
如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着B到点C的方向平移到△DEF的位置,AB=10,EH=7,平移距离是6,则图中阴影部分的面积为30.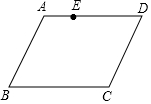 如图,点E是?ABCD边AD上一点,请你只用一把没有刻度的直尺,在BC边上确定一点F,使得CF=AE,请画出示意图,并用你学过的知识验证CF=AE.
如图,点E是?ABCD边AD上一点,请你只用一把没有刻度的直尺,在BC边上确定一点F,使得CF=AE,请画出示意图,并用你学过的知识验证CF=AE.