题目内容
17．若正方形的一条对角线长为4cm，则它的边长为2$\sqrt{2}$cm，面积为8cm2．分析 根据正方形性质可知：正方形的一条角平分线即为对角线，对角线和正方形的两条相邻的边构成等腰直角三角形，根据勾股定理可知正方形的边长，进而可得这个正方形的面积．
解答 解：设这个正方形的边长为xcm，
则根据正方形的性质可知：x2+x2=42=16，
解可得x=2$\sqrt{2}$cm；
则它的面积是x2=8cm2，
故答案为2$\sqrt{2}$，8．
点评 主要考查到正方形的性质和面积的求法．要注意：正方形的对角线和正方形的两条相邻的边构成等腰直角三角形．
练习册系列答案
相关题目
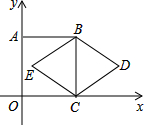如图，正方形ABCO的顶点C、A分别在x轴、y轴上，BC是菱形BDCE的对角线，若∠D=60°，BC=2，则点E的坐标是（2-$\sqrt{3}$，1）．
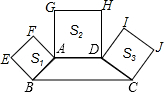如图，四边形ABCD中，AD∥BC，且∠B+∠C=90°，分别以AB、AD、DC为边向形外作正方形ABEF、正方形ADHG、正方形DCJI，且其面积依次记为S1、S2、S3，若S1+S3=4S2，求$\frac{BC}{AD}$的值．
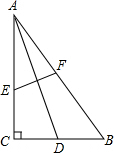如图，在Rt△ABC中，∠C=90°，AC=BC=2，AD是BC边上的中线，将A点翻折与点D重合，得到折痕EF，求CE：AE的值．
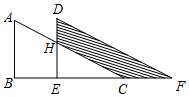如图，两个完全一样的直角三角形重叠在一起，将其中的一个三角形沿着B到点C的方向平移到△DEF的位置，AB=10，EH=7，平移距离是6，则图中阴影部分的面积为30．
