题目内容
18. 如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:
如图,正方形ABCD的边长为1,AC,BD是对角线.将△DCB绕着点D顺时针旋转45°得到△DGH,HG交AB于点E,连接DE交AC于点F,连接FG.则下列结论:①四边形AEGF是菱形 ②△AED≌△GED ③∠DFG=112.5°
④BC+FG=1.5,其中正确的结论是( )
| A. | ①②③④ | B. | ①②③ | C. | ①② | D. | ② |
分析 首先证明RT△ADE≌RT△GDE,再求出∠AEF、∠AFE、∠GEF、∠GFE的度数,推出AE=EG=FG=AF,由此可以一一判断.
解答  证明:∵四边形ABCD是正方形,
证明:∵四边形ABCD是正方形,
∴AD=DC=BC=AB,∠DAB=∠ADC=∠DCB=∠ABC=90°,∠ADB=∠BDC=∠CAD=∠CAB=45°,
∵△DHG是由△DBC旋转得到,
∴DG=DC=AD,∠DGE=∠DCB=∠DAE=90°,
在RT△ADE和RT△GDE中,
$\left\{\begin{array}{l}{DE=DE}\\{DA=DG}\end{array}\right.$,
∴RT△AED≌RT△GED,故②正确;
∴∠ADE=∠EDG=22.5°,AE=EG,
∴∠AED=∠AFE=67.5°,
∴AE=AF,
在△AEF与△GEF中,
$\left\{\begin{array}{l}{AE=EG}\\{EF=EF}\\{AF=GF}\end{array}\right.$,
△AEF≌△GEF,
∴EG=GF,
∴AE=EG=GF=FA,
∴四边形AEGF是菱形,故①正确;
∵∠DFG=∠GFC+∠DFC=∠BAC+∠DAC+∠ADF=112.5°,故③正确;
∵AE=FG=EG=BG,BE=$\sqrt{2}$AE,
∴BE>AE,
∴AE<$\frac{1}{2}$,
∴CB+FG<1.5,故④错误.
故选B.
点评 本题考查正方形的性质、全等三角形的判定和性质、菱形的判定和性质、等腰直角三角形的性质等知识,解题的关键是通过计算发现角相等,学会这种证明角相等的方法,属于中考常考题型.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
3.声音在空气中传播的速度与气温的关系如下表,根据表格分析下列说法错误的是( )
| 气温T/℃ | -20 | -10 | 0 | 10 | 20 | 30 |
| 声速v/m/s | 318 | 324 | 330 | 336 | 342 | 348 |
| A. | 在这个变化过程中,气温是自变量,声速是因变量 | |
| B. | 声速随气温的升高而增大 | |
| C. | 声速v与气温T的关系式为v=T+330 | |
| D. | 气温每升高10℃,声速增加6m/s |
10.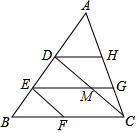 如图,DH∥EG∥BC,DC∥EF,那么与∠DCB相等的角的个数为( )
如图,DH∥EG∥BC,DC∥EF,那么与∠DCB相等的角的个数为( )
 如图,DH∥EG∥BC,DC∥EF,那么与∠DCB相等的角的个数为( )
如图,DH∥EG∥BC,DC∥EF,那么与∠DCB相等的角的个数为( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
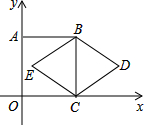 如图,正方形ABCO的顶点C、A分别在x轴、y轴上,BC是菱形BDCE的对角线,若∠D=60°,BC=2,则点E的坐标是(2-$\sqrt{3}$,1).
如图,正方形ABCO的顶点C、A分别在x轴、y轴上,BC是菱形BDCE的对角线,若∠D=60°,BC=2,则点E的坐标是(2-$\sqrt{3}$,1).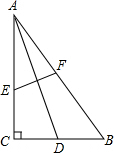 如图,在Rt△ABC中,∠C=90°,AC=BC=2,AD是BC边上的中线,将A点翻折与点D重合,得到折痕EF,求CE:AE的值.
如图,在Rt△ABC中,∠C=90°,AC=BC=2,AD是BC边上的中线,将A点翻折与点D重合,得到折痕EF,求CE:AE的值.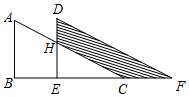 如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着B到点C的方向平移到△DEF的位置,AB=10,EH=7,平移距离是6,则图中阴影部分的面积为30.
如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着B到点C的方向平移到△DEF的位置,AB=10,EH=7,平移距离是6,则图中阴影部分的面积为30.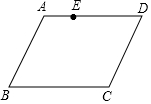 如图,点E是?ABCD边AD上一点,请你只用一把没有刻度的直尺,在BC边上确定一点F,使得CF=AE,请画出示意图,并用你学过的知识验证CF=AE.
如图,点E是?ABCD边AD上一点,请你只用一把没有刻度的直尺,在BC边上确定一点F,使得CF=AE,请画出示意图,并用你学过的知识验证CF=AE.



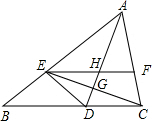 如图,AD是∠BAC平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F,AD与CE交于点G,与EF交于点H.
如图,AD是∠BAC平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F,AD与CE交于点G,与EF交于点H.