题目内容
10．已知抛物线y=x2-2x-8与x轴的两个交点分别为A、B（A在B的左边），且它的顶点为P，求△ABP的面积．分析 分别求出抛物线顶点P坐标，与x轴交点A、B坐标，即可解决问题．
解答 解：∵抛物线y=x2-2x-8，令y=0得x2-2x-8=0，∴x=4或-2，
∴点A（-2，0），点B（4，0），
∵y=（x-1）2-9，
∴顶点P（1，-9），
∴S△ABP=$\frac{1}{2}$×6×9=27．
点评 本题考查抛物线与x轴交点的有关知识、三角形面积公式，学会求抛物线与坐标轴的交点，会利用配方法求抛物线顶点坐标，属于中考常考题型．
练习册系列答案
相关题目
5．
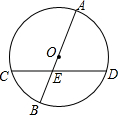如图，AB为⊙O的直径，CD为弦，AE=7cm，BE=3cm，∠AED=60°，则弦CD的长为（ ）
如图，AB为⊙O的直径，CD为弦，AE=7cm，BE=3cm，∠AED=60°，则弦CD的长为（ ）| A． | 2$\sqrt{21}$cm | B． | 4$\sqrt{6}$cm | C． | 2$\sqrt{22}$cm | D． | 8cm |
2．元旦期间，为了满足长丰县百姓的消费需要，某大型商场计划用170000元购进一批家电，这批家里的进价和售价如表：
若在现有资金允许的范围内，购买表中三类家电共100台，其中彩电台数是冰箱台数的2倍，设该商场购买冰箱x台．
（1）用含x的代数式表示洗衣机的台数．
（2）商场至多可以购买冰箱多少台？
（3）购买冰箱多少台时，能使商场销售完这批家电后获得的利润最大？最大利润为多少元？
| 类别 | 彩电 | 冰箱 | 洗衣机 |
| 进价（元/台） | 2000 | 1600 | 1000 |
| 售价（元/台） | 2300 | 1800 | 1100 |
（1）用含x的代数式表示洗衣机的台数．
（2）商场至多可以购买冰箱多少台？
（3）购买冰箱多少台时，能使商场销售完这批家电后获得的利润最大？最大利润为多少元？
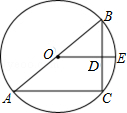如图，AB是⊙O的直径，BC是弦，点E是BC的中点，OE交BC于点D．连接AC，若BC=6，DE=1，求AC的长．