题目内容
19.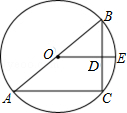 如图,AB是⊙O的直径,BC是弦,点E是BC的中点,OE交BC于点D.连接AC,若BC=6,DE=1,求AC的长.
如图,AB是⊙O的直径,BC是弦,点E是BC的中点,OE交BC于点D.连接AC,若BC=6,DE=1,求AC的长.
分析 连接OC,由垂径定理得出OD⊥BC,BD=CD.在直角三角形BDO中,根据勾股定理可求出OB,进而求出OD长,再根据三角形中位线定理可得AC的长.
解答 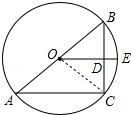 解:连接OC,如图所示.
解:连接OC,如图所示.
∵点E是$\widehat{BC}$的中点,
∴∠BOE=∠COE,OD⊥BC,BD=DC.
∵BC=6,
∴BD=3.
设⊙O的半径为r,则OB=OE=r.
∵DE=1,
∴OD=r-1.
∵OD⊥BC即∠BDO=90°,
∴OB2=BD2+OD2.
∵OB=r,OD=r-1,BD=3,
∴r2=32+(r-1)2.
解得:r=5.
∴OD=4.
∵AO=BO,BD=CD,
∴OD是△ABC的中位线,
∴OD=$\frac{1}{2}$AC.
∴AC=8.
点评 本题考查了垂径定理、勾股定理、三角形中位线定理等知识;熟练掌握垂径定理,由勾股定理求出半径是解决问题的关键.

练习册系列答案
相关题目
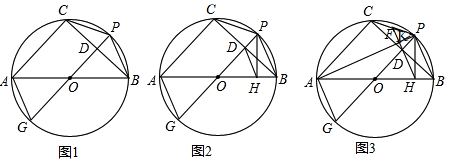
 如图,在⊙O中,直径AB=10,弦CD⊥AB,垂足为E,OE=3,求弦CD的长.
如图,在⊙O中,直径AB=10,弦CD⊥AB,垂足为E,OE=3,求弦CD的长.
 如图,已知在⊙O中,AB=3,AC是⊙O的直径,AC⊥BD于F,∠A=30°.
如图,已知在⊙O中,AB=3,AC是⊙O的直径,AC⊥BD于F,∠A=30°.