题目内容
15.(1)先化简,再求值:($\frac{x+1}{{x}^{2}-1}+\frac{x}{x-1}$)÷$\frac{x+1}{{x}^{2}-2x+1}$,其中x=2(2)已知xm=6,xn=3,试求x2m-3n的值.
分析 (1)先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可;
(2)根据同底数幂的除法法则进行计算即可.
解答 解:(1)原式=[$\frac{x+1}{(x+1)(x-1)}$+$\frac{x}{x-1}$]÷$\frac{x+1}{(x-1)^{2}}$
=[$\frac{1}{x-1}$+$\frac{x}{x-1}$]•$\frac{(x-1)^{2}}{x+1}$
=$\frac{x+1}{x-1}$•$\frac{{(x-1)}^{2}}{x+1}$
=x-1,
当x=2时,原式=1;
(2)∵xm=6,xn=3,
∴x2m-3n=$\frac{{x}^{2m}}{{x}^{3n}}$=$\frac{({x}^{m})^{2}}{({x}^{n})^{3}}$=$\frac{{6}^{2}}{{3}^{3}}$=$\frac{36}{27}$=$\frac{4}{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
6. 如图,四边形ABCD内接于⊙O,已知∠ADC=130°,则∠AOC的大小是( )
如图,四边形ABCD内接于⊙O,已知∠ADC=130°,则∠AOC的大小是( )
 如图,四边形ABCD内接于⊙O,已知∠ADC=130°,则∠AOC的大小是( )
如图,四边形ABCD内接于⊙O,已知∠ADC=130°,则∠AOC的大小是( )| A. | 80° | B. | 100° | C. | 60° | D. | 40° |
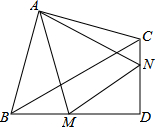 如图,在Rt△ABC和Rt△BCD中,∠BAC=∠BDC=90°,BC=8,AB=AC,∠CBD=30°,BD=4$\sqrt{3}$,M,N分别在BD,CD上,∠MAN=45°,则△DMN的周长为4$\sqrt{3}$+4.
如图,在Rt△ABC和Rt△BCD中,∠BAC=∠BDC=90°,BC=8,AB=AC,∠CBD=30°,BD=4$\sqrt{3}$,M,N分别在BD,CD上,∠MAN=45°,则△DMN的周长为4$\sqrt{3}$+4. 如图,在⊙O中,直径AB=10,弦CD⊥AB,垂足为E,OE=3,求弦CD的长.
如图,在⊙O中,直径AB=10,弦CD⊥AB,垂足为E,OE=3,求弦CD的长.