题目内容
1.用代入消元法求二元一次方程组$\left\{\begin{array}{l}{x+y=5}\\{2-2y=-1}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=\frac{7}{2}}\\{y=\frac{3}{2}}\end{array}\right.$.分析 由第二个方程求得y=$\frac{3}{2}$,然后代入第一个方程求出x的值即可.
解答 解:$\left\{\begin{array}{l}{x+y=5①}\\{2-2y=-1②}\end{array}\right.$,
由②得,2y=3,
解得y=$\frac{3}{2}$,
把y=$\frac{3}{2}$代入①得,x+$\frac{3}{2}$=5,
解得x=$\frac{7}{2}$,
所以,方程组的解是$\left\{\begin{array}{l}{x=\frac{7}{2}}\\{y=\frac{3}{2}}\end{array}\right.$;
故答案为$\left\{\begin{array}{l}{x=\frac{7}{2}}\\{y=\frac{3}{2}}\end{array}\right.$.
点评 本题考查的是二元一次方程组的解法,方程组中未知数的系数较小时可用代入法,当未知数的系数相等或互为相反数时用加减消元法较简单.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
16.设α,β为x2-x-1=0的两根,则$\frac{1}{α}$+$\frac{1}{β}$=( )
| A. | -1 | B. | 1 | C. | 0 | D. | 2 |
6. 如图,四边形ABCD内接于⊙O,已知∠ADC=130°,则∠AOC的大小是( )
如图,四边形ABCD内接于⊙O,已知∠ADC=130°,则∠AOC的大小是( )
 如图,四边形ABCD内接于⊙O,已知∠ADC=130°,则∠AOC的大小是( )
如图,四边形ABCD内接于⊙O,已知∠ADC=130°,则∠AOC的大小是( )| A. | 80° | B. | 100° | C. | 60° | D. | 40° |
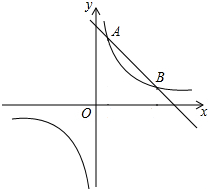 如图,直线y1=-x+b与双曲线y2=$\frac{8}{x}$交于A、B两点,点A的横坐标为1,则不等式-x+b<$\frac{8}{x}$的解集是0<x<1或x>8.
如图,直线y1=-x+b与双曲线y2=$\frac{8}{x}$交于A、B两点,点A的横坐标为1,则不等式-x+b<$\frac{8}{x}$的解集是0<x<1或x>8.