题目内容
19. 将一张三角形纸片ABC,沿AD进行折叠,点C的对应点E落在△ABC外面,DE交AB于点F,得到如图所示的多边形AEFBD,这个多边形的面积是△ABC面积的$\frac{13}{16}$.已知图中阴影部分的面积为50,则△ABC的面积为80.
将一张三角形纸片ABC,沿AD进行折叠,点C的对应点E落在△ABC外面,DE交AB于点F,得到如图所示的多边形AEFBD,这个多边形的面积是△ABC面积的$\frac{13}{16}$.已知图中阴影部分的面积为50,则△ABC的面积为80.
分析 设△BDF的面积为x,△AEF的面积为y,△AFD的面积为z,要求△ABC的面积就是要求x+y+2z,因为x+y=50,所以只要求出z,列出方程组即可解决这个问题.
解答 解:设△BDF的面积为x,△AEF的面积为y,△AFD的面积为z.
∵△ADE是由△ADC翻折,
∴△ADC的面积为y+z,△ABC的面积为x+y+2z.
由题意$\left\{\begin{array}{l}{x+y=50}\\{x+y+z=\frac{13}{16}(x+y+2z)}\end{array}\right.$解得到:z=15,
∴△ABC的面积=50+2×15=80.
故答案为80.
点评 本题考查翻折变换、三角形面积问题等知识,解题的关键是把问题转化为方程组,体现了数形结合的思想,是一条好题目.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
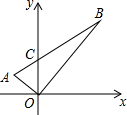 如图,在直角坐标平面上,△AOB是直角三角形,点O在原点上,A、B两点的坐标分别为(-1,y1)、(3,y2),线段AB交y轴于点C.若S△AOC=1,记∠AOC为α,∠BOC为β,则sinα•sinβ的值为$\frac{3}{8}$.
如图,在直角坐标平面上,△AOB是直角三角形,点O在原点上,A、B两点的坐标分别为(-1,y1)、(3,y2),线段AB交y轴于点C.若S△AOC=1,记∠AOC为α,∠BOC为β,则sinα•sinβ的值为$\frac{3}{8}$.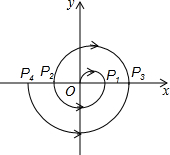 如图,在平面直角坐标系中,设一动点P自原点O处开始顺时针运动,沿半径为1个单位长度的半圆运动至x轴,记为点P1;再沿半径为2个单位长度的半圆运动至x轴,记为点P2;再沿半径为3个单位长度的半圆运动至x轴,记为点P3,…如此继续运动下去,当点P运动到点P302处时,点P所运动的路程为45753π.(结果保留π)
如图,在平面直角坐标系中,设一动点P自原点O处开始顺时针运动,沿半径为1个单位长度的半圆运动至x轴,记为点P1;再沿半径为2个单位长度的半圆运动至x轴,记为点P2;再沿半径为3个单位长度的半圆运动至x轴,记为点P3,…如此继续运动下去,当点P运动到点P302处时,点P所运动的路程为45753π.(结果保留π) 如图,抛物线y=-x2+bx+c与直线AB相交于A(-1,0)、B(2,3)两点,与y轴交于点C,其顶点为D.
如图,抛物线y=-x2+bx+c与直线AB相交于A(-1,0)、B(2,3)两点,与y轴交于点C,其顶点为D.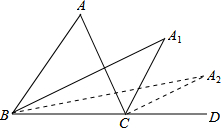 如图,已知△ABC的内角∠A=α°,分别作内角∠ABC与外角∠ACD的平分线,两条平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…以此类推得到∠A2014,则∠A2014的度数是$\frac{1}{{2}^{2014}}$α.
如图,已知△ABC的内角∠A=α°,分别作内角∠ABC与外角∠ACD的平分线,两条平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;…以此类推得到∠A2014,则∠A2014的度数是$\frac{1}{{2}^{2014}}$α.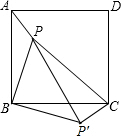 如图,点P是正方形ABCD内的一点,连接AP,BP,CP.将△PAB绕着点B顺时针旋转90°到△P′CB的位置,若AP=2,BP=4,∠APB=135°.求PP′及PC的长.
如图,点P是正方形ABCD内的一点,连接AP,BP,CP.将△PAB绕着点B顺时针旋转90°到△P′CB的位置,若AP=2,BP=4,∠APB=135°.求PP′及PC的长.