题目内容
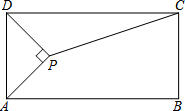 如图,矩形ABCD中,AP平分∠DAB,且AP⊥DP于点P,联结CP,如果AB﹦8,AD﹦4,求sin∠DCP的值.
如图,矩形ABCD中,AP平分∠DAB,且AP⊥DP于点P,联结CP,如果AB﹦8,AD﹦4,求sin∠DCP的值.考点:解直角三角形
专题:
分析:过点P作PE⊥CD于点E,根据已知得出∠DAP=∠ADP=∠CDP=45°,在Rt△APD中通过正弦函数值求得DP,然后在Rt△DEP中根据正弦函数值求得PE、DE,进而求得CE,在Rt△DEP中,根据勾股定理求得PC,进而即可求得sin∠DCP的值.
解答: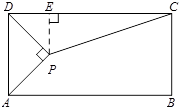 解:过点P作PE⊥CD于点E,
解:过点P作PE⊥CD于点E,
∵四边形ABCD是矩形,
∴CD=AB=8,∠DAB=∠ADC=90°.
∵AP是∠DAB的角平分线,
∴∠DAP=
∠DAB=45°.
∵DP⊥AP,
∴∠APD=90°.
∴∠ADP=45°.
∴∠CDP=45°.
在Rt△APD中,AD=4,
∴DP=AD•sin∠DAP=2
,
在Rt△DEP中,∠DEP=90°,
∴PE=DP•sin∠CDP=2,DE=DP•cos∠CDP=2.
∴CE=CD-DE=6,
在Rt△DEP中,∠CEP=90°,PC=
=2
,
∴sin∠DCP=
=
.
 解:过点P作PE⊥CD于点E,
解:过点P作PE⊥CD于点E,∵四边形ABCD是矩形,
∴CD=AB=8,∠DAB=∠ADC=90°.
∵AP是∠DAB的角平分线,
∴∠DAP=
| 1 |
| 2 |
∵DP⊥AP,
∴∠APD=90°.
∴∠ADP=45°.
∴∠CDP=45°.
在Rt△APD中,AD=4,
∴DP=AD•sin∠DAP=2
| 2 |
在Rt△DEP中,∠DEP=90°,
∴PE=DP•sin∠CDP=2,DE=DP•cos∠CDP=2.
∴CE=CD-DE=6,
在Rt△DEP中,∠CEP=90°,PC=
| CE2+PE2 |
| 10 |
∴sin∠DCP=
| PE |
| PC |
| ||
| 10 |
点评:本题考查了直角三角形函数以及勾股定理,作出辅助线构建直角三角形是本题的关键.

练习册系列答案
相关题目
已知点(-1,y1),(3,y2),(
,y3)在函数y=x2+2x+m的图象上,则y1,y2,y3的大小关系是( )
| 1 |
| 2 |
| A、y1>y2>y3 |
| B、y2>y1>y3 |
| C、y2>y3>y1 |
| D、y3>y1>y2 |
通常来讲,电视机的大小是以屏幕的对角线长度来测量的(1英寸≈2.5厘米)现有一台电视机的屏幕长约80厘米,宽约60厘米,则该电视机的大小是( )
| A、25英寸 | B、29英寸 |
| C、34英寸 | D、40英寸 |
 已知在数轴上有A,B两点,点A表示的数为8,点B在A点的左边,且AB=12.若有一动点P从数轴上点A出发,以每秒3个单位长度的速度沿数轴向左匀速运动,动点Q从点B出发,以每秒2个单位长度的速度沿着数轴向右匀速运动,设运动时间为t秒.
已知在数轴上有A,B两点,点A表示的数为8,点B在A点的左边,且AB=12.若有一动点P从数轴上点A出发,以每秒3个单位长度的速度沿数轴向左匀速运动,动点Q从点B出发,以每秒2个单位长度的速度沿着数轴向右匀速运动,设运动时间为t秒. 如图,在Rt△ABC中,∠ACB=90°,CA=CB,AB=4,CD⊥AB,垂足为D,则CD的长为
如图,在Rt△ABC中,∠ACB=90°,CA=CB,AB=4,CD⊥AB,垂足为D,则CD的长为