题目内容
 如图,在Rt△ABC中,∠ACB=90°,CA=CB,AB=4,CD⊥AB,垂足为D,则CD的长为
如图,在Rt△ABC中,∠ACB=90°,CA=CB,AB=4,CD⊥AB,垂足为D,则CD的长为考点:等腰直角三角形
专题:
分析:由已知可得Rt△ABC是等腰直角三角形,得出AD=BD=
AB=2,再由直角三角形斜边的中线等于斜边的一半得出CD=BD=2.
| 1 |
| 2 |
解答:解:∵∠ACB=90°,CA=CB,
∴∠A=∠B=45°,
∵CD⊥AB,
∴AD=BD=
AB=2,∠CDB=90°,
∴CD=BD=2.
故答案为2.
∴∠A=∠B=45°,
∵CD⊥AB,
∴AD=BD=
| 1 |
| 2 |
∴CD=BD=2.
故答案为2.
点评:本题主要考查了等腰直角三角形,解题的关键是灵活运用等腰直角三角形的性质求角及边的关系.

练习册系列答案
相关题目
 已知有理数a,b,c在数轴上的位置如图所示,则化简代数式|b-c|-|c-a|+|b-a|=
已知有理数a,b,c在数轴上的位置如图所示,则化简代数式|b-c|-|c-a|+|b-a|=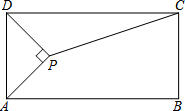 如图,矩形ABCD中,AP平分∠DAB,且AP⊥DP于点P,联结CP,如果AB﹦8,AD﹦4,求sin∠DCP的值.
如图,矩形ABCD中,AP平分∠DAB,且AP⊥DP于点P,联结CP,如果AB﹦8,AD﹦4,求sin∠DCP的值. (1)在方格纸上过点P作线段AB的平行线l;
(1)在方格纸上过点P作线段AB的平行线l;