题目内容
已知点(-1,y1),(3,y2),(
,y3)在函数y=x2+2x+m的图象上,则y1,y2,y3的大小关系是( )
| 1 |
| 2 |
| A、y1>y2>y3 |
| B、y2>y1>y3 |
| C、y2>y3>y1 |
| D、y3>y1>y2 |
考点:二次函数图象上点的坐标特征
专题:
分析:先求得抛物线的对称轴为直线x=-1,根据二次函数的性质,通过三点与对称轴距离的远近来比较函数值的大小.
解答:解:∵由函数y=x2+2x+m可知则抛物线的对称轴为直线x=-1,开口向上,而点A(-1,y1)在对称轴上,(3,y2)、(
,y3))在对称轴的右侧,
∴y2>y3>y1.
故选C.
| 1 |
| 2 |
∴y2>y3>y1.
故选C.
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.

练习册系列答案
相关题目
在3-
,
,
,0.202 002 000 2,
中,无理数的个数有( )
| 11 |
| 23 |
| 7 |
| π |
| 3 |
| 23 |
| A、6个 | B、5个 | C、4个 | D、3个 |
下列说法中:
①法国数学家笛卡尔首先建立了坐标思想
②全等三角形对应边上的中线长相等
③若a2>b2,则a>b
④有两边和其中一条边所对的一个角对应相等的两个三角形一定全等,
说法正确的为( )
①法国数学家笛卡尔首先建立了坐标思想
②全等三角形对应边上的中线长相等
③若a2>b2,则a>b
④有两边和其中一条边所对的一个角对应相等的两个三角形一定全等,
说法正确的为( )
| A、①② | B、②④ |
| C、②③④ | D、①③④ |
 如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C,若∠A=60°,∠B=110°,则∠BCA′的度数是( )
如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C,若∠A=60°,∠B=110°,则∠BCA′的度数是( )| A、60° | B、80° |
| C、40° | D、30° |
根据等式的性质下列变形正确的是( )
A、由
| ||||
B、
| ||||
C、由-2x=-3,得x=
| ||||
D、由
|
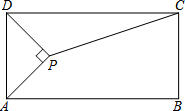 如图,矩形ABCD中,AP平分∠DAB,且AP⊥DP于点P,联结CP,如果AB﹦8,AD﹦4,求sin∠DCP的值.
如图,矩形ABCD中,AP平分∠DAB,且AP⊥DP于点P,联结CP,如果AB﹦8,AD﹦4,求sin∠DCP的值.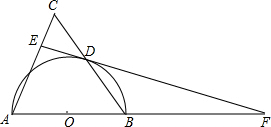 如图,在△ABC中,AB=AC,以AB为直径作半圆⊙0,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.
如图,在△ABC中,AB=AC,以AB为直径作半圆⊙0,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F. (1)在方格纸上过点P作线段AB的平行线l;
(1)在方格纸上过点P作线段AB的平行线l;