题目内容
通常来讲,电视机的大小是以屏幕的对角线长度来测量的(1英寸≈2.5厘米)现有一台电视机的屏幕长约80厘米,宽约60厘米,则该电视机的大小是( )
| A、25英寸 | B、29英寸 |
| C、34英寸 | D、40英寸 |
考点:勾股定理的应用
专题:
分析:根据勾股定理求出电视机对角线的长即可.
解答:解:∵一台电视机的屏幕长约80厘米,宽约60厘米,
∴对角线的长=
=100.
∵1英寸≈2.5厘米,
∴
=40(英寸).
故选D.
∴对角线的长=
| 802+602 |
∵1英寸≈2.5厘米,
∴
| 100 |
| 2.5 |
故选D.
点评:本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
相关题目
 如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C,若∠A=60°,∠B=110°,则∠BCA′的度数是( )
如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C,若∠A=60°,∠B=110°,则∠BCA′的度数是( )| A、60° | B、80° |
| C、40° | D、30° |
下列说法正确的是( )
| A、若MN=2MC,则点C是线段MN的中点 |
| B、点到直线的距离是指从直线外一点到这条直线的垂线的长度 |
| C、有AB=MA+MB,AB<NA+NB,则点M在线段AB上,点N在线段AB外 |
| D、一条射线把一个角分成两个角,这条射线是这个角的平分线 |
根据等式的性质下列变形正确的是( )
A、由
| ||||
B、
| ||||
C、由-2x=-3,得x=
| ||||
D、由
|
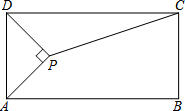 如图,矩形ABCD中,AP平分∠DAB,且AP⊥DP于点P,联结CP,如果AB﹦8,AD﹦4,求sin∠DCP的值.
如图,矩形ABCD中,AP平分∠DAB,且AP⊥DP于点P,联结CP,如果AB﹦8,AD﹦4,求sin∠DCP的值. (1)在方格纸上过点P作线段AB的平行线l;
(1)在方格纸上过点P作线段AB的平行线l;