题目内容
6.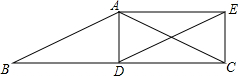 如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD、CE.
如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD、CE.(1)求证:△ACD≌△EDC;
(2)若点D是BC中点,说明四边形ADCE是矩形.
分析 (1)根据平行四边形的性质、等腰三角形的性质,利用全等三角形的判定定理SAS可以证得△ADC≌△ECD;
(2)利用等腰三角形的“三合一”性质推知AD⊥BC,即∠ADC=90°;由平行四边形的判定定理(一组对边平行且相等的四边形是平行四边形)证得四边形ADCE是平行四边形,所以有一个角是直角的平行四边形是矩形.
解答 证明:(1)∵四边形ABDE是平行四边形(已知),
∴AB∥DE,AB=DE(平行四边形的对边平行且相等);
∴∠B=∠EDC(两直线平行,同位角相等);
又∵AB=AC(已知),
∴AC=DE(等量代换),∠B=∠ACB(等边对等角),
∴∠EDC=∠ACD(等量代换);
∵在△ADC和△ECD中,
$\left\{\begin{array}{l}{AC=ED}\\{∠ACD=∠EDC}\\{DC=CD}\end{array}\right.$,
∴△ADC≌△ECD(SAS);
(2)∵四边形ABDE是平行四边形(已知),
∴BD∥AE,BD=AE(平行四边形的对边平行且相等),
∴AE∥CD,
∵点D是BC中点,
∴BD=CD,
∴AE=CD(等量代换),
∴四边形ADCE是平行四边形(一组对边平行且相等的四边形是平行四边形);
在△ABC中,AB=AC,BD=CD,
∴AD⊥BC(等腰三角形的“三线合一”性质),
∴∠ADC=90°,
∴四边形ADCE是矩形.
点评 本题综合考查了平行四边形的判定与性质、全等三角形的判定以及矩形的判定.注意:矩形的判定定理是“有一个角是直角的‘平行四边形’是矩形”,而不是“有一个角是直角的‘四边形’是矩形”.

练习册系列答案
相关题目
11.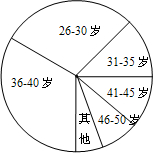 2012年3月全国两会在北京召开,公众最关心哪些问题?九一班学生就老百姓最关注的两会热点问题,在网络上发布了相应的调查问卷,到目前为止,共有不同年龄段的2880人参与,其中31~35岁关心问题的具体情况统计如下:
2012年3月全国两会在北京召开,公众最关心哪些问题?九一班学生就老百姓最关注的两会热点问题,在网络上发布了相应的调查问卷,到目前为止,共有不同年龄段的2880人参与,其中31~35岁关心问题的具体情况统计如下:
(1)请将统计表中遗漏的数据补上;
(2)求扇形图(如图)中表示31~35岁的扇形的圆心角的度数;
(3)在参加调查的31~35岁段中随机抽取一人,关心物价调控或医疗改革的概率是多少?
 2012年3月全国两会在北京召开,公众最关心哪些问题?九一班学生就老百姓最关注的两会热点问题,在网络上发布了相应的调查问卷,到目前为止,共有不同年龄段的2880人参与,其中31~35岁关心问题的具体情况统计如下:
2012年3月全国两会在北京召开,公众最关心哪些问题?九一班学生就老百姓最关注的两会热点问题,在网络上发布了相应的调查问卷,到目前为止,共有不同年龄段的2880人参与,其中31~35岁关心问题的具体情况统计如下:| 关心问题 | 频数 | 频率 |
| 收入分配 | 90 | 0.25 |
| 住房问题 | 54 | 0.15 |
| 物价调控 | 36 | 0.1 |
| 医疗改革 | 18 | 0.05 |
| 养老保险 | 54 | 0.15 |
| 其他 | 108 | 0.30 |
| 合计 | 360 | 1 |
(2)求扇形图(如图)中表示31~35岁的扇形的圆心角的度数;
(3)在参加调查的31~35岁段中随机抽取一人,关心物价调控或医疗改革的概率是多少?
18. 如图,菱形ABCD由6个腰长为3,且全等的等腰梯形镶嵌而成,则线段AC的长为( )
如图,菱形ABCD由6个腰长为3,且全等的等腰梯形镶嵌而成,则线段AC的长为( )
 如图,菱形ABCD由6个腰长为3,且全等的等腰梯形镶嵌而成,则线段AC的长为( )
如图,菱形ABCD由6个腰长为3,且全等的等腰梯形镶嵌而成,则线段AC的长为( )| A. | 6 | B. | 9$\sqrt{2}$ | C. | 6$\sqrt{3}$ | D. | 9$\sqrt{3}$ |
15.已知a>b,下列四个不等式中不正确的是( )
| A. | 4a>4b | B. | -4a<-4b | C. | a+4>b+4 | D. | a-4<b-4 |
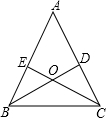 已知:如图,锐角△ABC的两条高BD、CE相交于点O,且BE=CD.
已知:如图,锐角△ABC的两条高BD、CE相交于点O,且BE=CD.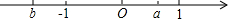 实数a、b在数轴上的位置如图所示,写出不等式组$\left\{\begin{array}{l}x+a>0\\ x-b>0\end{array}$的解集为x>-a.
实数a、b在数轴上的位置如图所示,写出不等式组$\left\{\begin{array}{l}x+a>0\\ x-b>0\end{array}$的解集为x>-a. 如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°.
如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O上一点,且∠AED=45°. 填空:如图,请你选择合适的条件填入空格中,使两个三角形全等.
填空:如图,请你选择合适的条件填入空格中,使两个三角形全等.