题目内容
18. 如图,菱形ABCD由6个腰长为3,且全等的等腰梯形镶嵌而成,则线段AC的长为( )
如图,菱形ABCD由6个腰长为3,且全等的等腰梯形镶嵌而成,则线段AC的长为( )| A. | 6 | B. | 9$\sqrt{2}$ | C. | 6$\sqrt{3}$ | D. | 9$\sqrt{3}$ |
分析 连结AC、BD,它们相交于O点,如图,根据菱形的性质得AC⊥BD,OA=OC,CD=CB,由于菱形ABCD由6个腰长为3,且全等的等腰梯形镶嵌而成,所以∠BCD=∠CDB,因式可判断△BDC为等边三角形,而BD=9,然后根据等边三角形的性质求得OC=$\frac{\sqrt{3}}{2}$BD=$\frac{9\sqrt{3}}{2}$,从而可得到AC的长.
解答 解:连结AC、BD,它们相交于O点,如图,
∵四边形ABCD为菱形,
∴AC⊥BD,OA=OC,CD=CB,
∵∠BCD=∠CDB,
∴△BDC为等边三角形,
而BD=3+3+3=9,
∴OC=$\frac{\sqrt{3}}{2}$BD=$\frac{9\sqrt{3}}{2}$,
∴AC=2OC=9$\sqrt{3}$.
故选D.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.也考查了等腰梯形的性质.

练习册系列答案
相关题目
8. 将一根24cm长的筷子置于底面直径为8cm,内部深度为15cm的圆柱形水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是( )
将一根24cm长的筷子置于底面直径为8cm,内部深度为15cm的圆柱形水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是( )
 将一根24cm长的筷子置于底面直径为8cm,内部深度为15cm的圆柱形水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是( )
将一根24cm长的筷子置于底面直径为8cm,内部深度为15cm的圆柱形水杯中,设筷子露在杯子外面的长度为hcm,则h的取值范围是( )| A. | h≥7cm | B. | h≤16cm | C. | 7cm≤h≤9cm | D. | 7cm≤h≤16cm |
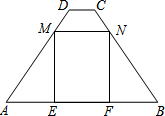 如图,在梯形ABCD中,AB∥CD,AB=7,CD=1,AD=BC=5.点M、N分别在边AD、BC上运动,并保持MN∥AB,ME⊥AB,NF⊥AB,垂足分别为E、F
如图,在梯形ABCD中,AB∥CD,AB=7,CD=1,AD=BC=5.点M、N分别在边AD、BC上运动,并保持MN∥AB,ME⊥AB,NF⊥AB,垂足分别为E、F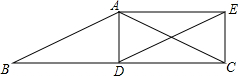 如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD、CE.
如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD、CE.
 如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为50°.
如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为50°.