题目内容
16.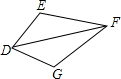 填空:如图,请你选择合适的条件填入空格中,使两个三角形全等.
填空:如图,请你选择合适的条件填入空格中,使两个三角形全等.①因为DF=DF,∠EDF=∠GDF,DE=DG,根据SAS,可知△DEF≌△DGF.
②因为DF=DF,∠EFD=∠GFD,,EF=FG,根据SAS,可知△DEF≌△DGF.
分析 ①添加条件∠EDF=∠GDF,DE=DG,根据SAS推出即可;
②添加条件∠EFD=∠GFD,EF=FG,根据SAS推出即可.
解答 解:①∠EDF=∠GDF,DE=DG,
理由是:∵在△DEF和△DGF中
$\left\{\begin{array}{l}{DF=DF}\\{∠EDF=∠GDF}\\{DE=DG}\end{array}\right.$
∴△DEF≌△DGF(SAS),
故答案为:∠EDF=∠GDF,DE=DG,SAS;
②∠EFD=∠GFD,EF=FG,
理由是:∵在△DEF和△DGF中
$\left\{\begin{array}{l}{DF=DF}\\{∠EFD=∠GFD}\\{EF=FG}\end{array}\right.$
∴△DEF≌△DGF(SAS),
故答案为:∠EFD=∠GFD,EF=FG,SAS.
点评 本题考查了全等三角形的判定的应用,能熟练地运用定理进行推理是解此题的关键,注意:全等三角形的判定定理有SAS,AAS,ASA,SSS,直角三角形全等的判定定理除了具有以上定理外,还有HL定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11. 如图,⊙O是△ABC的外接圆,且∠BAO=25°,则∠C的大小为( )
如图,⊙O是△ABC的外接圆,且∠BAO=25°,则∠C的大小为( )
 如图,⊙O是△ABC的外接圆,且∠BAO=25°,则∠C的大小为( )
如图,⊙O是△ABC的外接圆,且∠BAO=25°,则∠C的大小为( )| A. | 25° | B. | 50° | C. | 60° | D. | 65° |
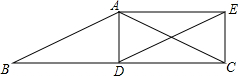 如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD、CE.
如图,在△ABC中,AB=AC,D为边BC上一点,以AB,BD为邻边作平行四边形ABDE,连接AD、CE.
 如图,在长方形ABCD中,AB>BC,BE⊥AC,垂足为E,延长BE交CD于F,S表示面积,则给出的下列命题:
如图,在长方形ABCD中,AB>BC,BE⊥AC,垂足为E,延长BE交CD于F,S表示面积,则给出的下列命题: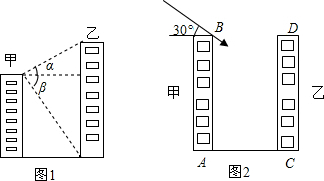
 如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为50°.
如图,在⊙O中,AC∥OB,∠BAO=25°,则∠BOC的度数为50°.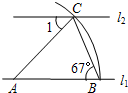 如图,直线l1∥l2,以直线l1上的点A为圆心、适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC.若∠ABC=67°,则∠1=46°.
如图,直线l1∥l2,以直线l1上的点A为圆心、适当长为半径画弧,分别交直线l1、l2于点B、C,连接AC、BC.若∠ABC=67°,则∠1=46°.