题目内容
1.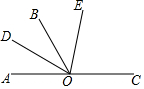 如图,已知O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,∠BOE=$\frac{1}{2}$∠EOC,∠DOE=70°,求∠EOC的度数.
如图,已知O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,∠BOE=$\frac{1}{2}$∠EOC,∠DOE=70°,求∠EOC的度数.
分析 设∠BOE=x°,则∠EOC=2x°,由∠DOE=70°及OD平分∠AOB知∠AOD=∠DOB=70°-x°,根据∠AOD+∠DOB+∠BOE+∠EOC=180°列出关于x的方程,解之可得.
解答 解:如图,设∠BOE=x°,
∵∠BOE=$\frac{1}{2}$∠EOC,
∴∠EOC=2x°,
∵OD平分∠AOB,
∴∠AOD=∠DOB=70°-x°,
∵∠AOD+∠DOB+∠BOE+∠EOC=180°,
∴70°-x+70°-x+x°+2x°=180°,
∴x=40,
∴∠EOC=80°.
点评 本题主要考查角的计算及角平分线的定义,熟练掌握角平分线的定义及性质是解题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案
相关题目
6.根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从2015年5月1日起对居民生活用电试行“阶梯电价”收费,具体收费标准见表:
若2015年5月份,该市居民甲用电100度,交电费60元.
(1)上表中,a=0.6;若居民乙用电200度,则应交电费122.5元;
(2)若某用户某月用电量超过300度,设用电量为x度,请你用含x的代数式表示应交的电费;
(3)试行“阶梯电价”收费以后,该市一户居民月用电多少度时,其当月的平均电价为每度0.62元?
| 一户居民一个月用电量的范围 | 电费价格(单位:元/度) |
| 不超过150度 | a |
| 超过150度但不超过300度的部分 | 0.65 |
| 超过300度的部分 | 0.9 |
(1)上表中,a=0.6;若居民乙用电200度,则应交电费122.5元;
(2)若某用户某月用电量超过300度,设用电量为x度,请你用含x的代数式表示应交的电费;
(3)试行“阶梯电价”收费以后,该市一户居民月用电多少度时,其当月的平均电价为每度0.62元?
 如图,在平面直角坐标系中,点A,B,C的坐标为(1,4),(5,4),(1,-2),则△ABC外接圆的圆心坐标是(3,1).
如图,在平面直角坐标系中,点A,B,C的坐标为(1,4),(5,4),(1,-2),则△ABC外接圆的圆心坐标是(3,1). 一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )
一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )