题目内容
10. 如图,在平面直角坐标系中,点A,B,C的坐标为(1,4),(5,4),(1,-2),则△ABC外接圆的圆心坐标是(3,1).
如图,在平面直角坐标系中,点A,B,C的坐标为(1,4),(5,4),(1,-2),则△ABC外接圆的圆心坐标是(3,1).
分析 根据点A,B的坐标求出线段AB的垂直平分线方程,同理得到线段AC的垂直平分线方程,根据三角形的外心的定义解答即可.
解答 解:∵点A,B的坐标为(1,4),(5,4),
∴线段AB的垂直平分线方程为x=3,
同理,线段AC的垂直平分线方程为y=1,
∴△ABC外接圆的圆心坐标是(3,1),
故答案为:(3,1).
点评 本题考查的是三角形的外接圆、坐标与图形性质,掌握三角形的外接圆的圆心是三角形的三边垂直平分线的交点是解题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
15.若点M(-3,2)和点N(a,b)关于y轴对称,则$\frac{b}{a}$的值为( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | -$\frac{3}{2}$ |
20.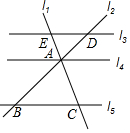 如图,l3∥l4∥l5,l1交l3,l4,l5于E,A,C,l2交l3,l4,l5于D,A,B,以下结论的错误的为( )
如图,l3∥l4∥l5,l1交l3,l4,l5于E,A,C,l2交l3,l4,l5于D,A,B,以下结论的错误的为( )
 如图,l3∥l4∥l5,l1交l3,l4,l5于E,A,C,l2交l3,l4,l5于D,A,B,以下结论的错误的为( )
如图,l3∥l4∥l5,l1交l3,l4,l5于E,A,C,l2交l3,l4,l5于D,A,B,以下结论的错误的为( )| A. | $\frac{EA}{AC}$=$\frac{DA}{AB}$ | B. | $\frac{BA}{BD}$=$\frac{CA}{CE}$ | C. | $\frac{CA}{CE}$=$\frac{DA}{DB}$ | D. | $\frac{EA}{EC}$=$\frac{DA}{DB}$ |
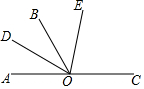 如图,已知O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,∠BOE=$\frac{1}{2}$∠EOC,∠DOE=70°,求∠EOC的度数.
如图,已知O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,∠BOE=$\frac{1}{2}$∠EOC,∠DOE=70°,求∠EOC的度数. 如图是每个面上都有一个汉字的正方体的表面展开图,那么在原正方体的表面上与汉字“爱”相对的面上的汉字是丽.
如图是每个面上都有一个汉字的正方体的表面展开图,那么在原正方体的表面上与汉字“爱”相对的面上的汉字是丽.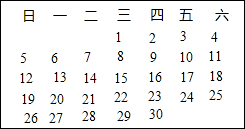 在如图的2016年6月份的月历表中,任意框出表中竖列上三个相邻的数,下面列出的这三个数的和①24,②35,③51,④72,其中不可能的是( )
在如图的2016年6月份的月历表中,任意框出表中竖列上三个相邻的数,下面列出的这三个数的和①24,②35,③51,④72,其中不可能的是( )