题目内容
11.解方程:(1)x2-5x-14=0
(2)3x2+1=2$\sqrt{3}$x.
分析 (1)方程等号右边为0,一次项系数是奇数,考虑十字相乘法或公式法;(2)把方程变形,使方程的右边为0,由于3=($\sqrt{3}$)2,中间一项是2$\sqrt{3}$x,考虑因式分解法或配方法.
解答 解:(1)x2-5x-14=0
(x-7)(x+2)=0
所以x-7=0或x+2=0
解得:x1=7,x2=-2.
(2)($\sqrt{3}$x)2-2$\sqrt{3}$x+1=0,
($\sqrt{3}$x-1)2=0
$\sqrt{3}x-1=0$
所以x1=x2=$\frac{\sqrt{3}}{3}$.
点评 本题考查了一元二次方程的解法.在一元二次方程的解法中,直接开平方法是基础,公式法适合所有的一元二次方程,因式分解法比较简单.

练习册系列答案
相关题目
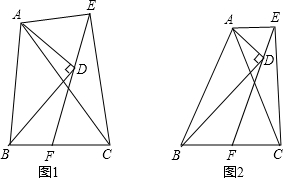
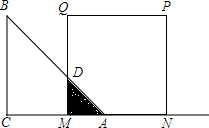 如图,等腰Rt△ABC(∠C=90°)与正方形MNPQ中,AC=MN=4,点A从M点位置出发向右运动,直到C与N点重合为止,设△ABC与正方形MNPQ的重叠部分面积为y,MA=x,则y与x之间的函数解析式为:y=$\left\{\begin{array}{l}{\frac{1}{2}{x}^{2}(0<x≤4)}\\{-\frac{1}{2}{x}^{2}+4x(4<x≤8)}\end{array}\right.$.
如图,等腰Rt△ABC(∠C=90°)与正方形MNPQ中,AC=MN=4,点A从M点位置出发向右运动,直到C与N点重合为止,设△ABC与正方形MNPQ的重叠部分面积为y,MA=x,则y与x之间的函数解析式为:y=$\left\{\begin{array}{l}{\frac{1}{2}{x}^{2}(0<x≤4)}\\{-\frac{1}{2}{x}^{2}+4x(4<x≤8)}\end{array}\right.$.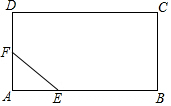 如图,有一块矩形钢板ABCD,先截去了一个直角三角形AEF,得到一个五边形EBCDF,已知AB=200cm,BC=160cm,AE=60cm,AF=40cm,要从这块钢板上再截出一块矩形板料,如何设计才能使矩形板料的面积最大?最大面积是多少?
如图,有一块矩形钢板ABCD,先截去了一个直角三角形AEF,得到一个五边形EBCDF,已知AB=200cm,BC=160cm,AE=60cm,AF=40cm,要从这块钢板上再截出一块矩形板料,如何设计才能使矩形板料的面积最大?最大面积是多少?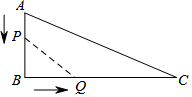 如图,在△ABC中,∠B=90°,AB=12cm,BC=24cm,动点P从点A开始沿边AB向B以2cm/s的速度移动,动点Q从点B开始沿BC边向C以4cm/s的速度移动,如果P、Q分别从A、B同时出发,设运动时间为t,△PBQ的面积为S.
如图,在△ABC中,∠B=90°,AB=12cm,BC=24cm,动点P从点A开始沿边AB向B以2cm/s的速度移动,动点Q从点B开始沿BC边向C以4cm/s的速度移动,如果P、Q分别从A、B同时出发,设运动时间为t,△PBQ的面积为S. 如图,在矩形ABCD中,AB=3,AD=4,若以点A为圆心,以4为半径作⊙A,则点A,点B,点C,点D四点中在⊙A外的是C.
如图,在矩形ABCD中,AB=3,AD=4,若以点A为圆心,以4为半径作⊙A,则点A,点B,点C,点D四点中在⊙A外的是C.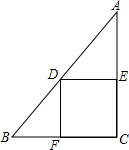 如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为点E,F,得四边形DECF,设DE=x,DF=y.
如图,在Rt△ABC中,∠C=90°,∠A=30°,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为点E,F,得四边形DECF,设DE=x,DF=y.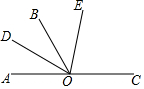 如图,已知O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,∠BOE=$\frac{1}{2}$∠EOC,∠DOE=70°,求∠EOC的度数.
如图,已知O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内,∠BOE=$\frac{1}{2}$∠EOC,∠DOE=70°,求∠EOC的度数.