题目内容
16.等边三角形ABC的两顶点A、B的坐标分别为(-2,0),(2,0),则点C的坐标为(0,2$\sqrt{3}$)或(0,-2$\sqrt{3}$).分析 设C点坐标为(x,y),根据三线合一可得C横坐标,再根据勾股定理可求得C的纵坐标,即可解题.
解答 解:设C点坐标为(x,y)
∵等边△ABC的顶点A(-2,0),B(2,0),
根据三线合一可得顶点C的横坐标为0,
∵AB=4,
∴AC=4
根据勾股定理可得42=22+y2,
解得y=±2$\sqrt{3}$,
∴顶点C的坐标为(0,2$\sqrt{3}$)或(0,-2$\sqrt{3}$).
故答案为(0,2$\sqrt{3}$)或(0,-2$\sqrt{3}$).
点评 本题考查了等边三角形的三线合一的性质,本题中熟练运用坐标系是解题的关键.

练习册系列答案
相关题目
6.铅笔的单价是a元,圆珠笔的单价是铅笔单价的3倍,则圆珠笔的单价是( )元.
| A. | 3a | B. | 3+a | C. | a-3 | D. | $\frac{a}{3}$ |
7. 如图,小波在周末时随父母到郊外放风筝,已知风筝线与水平线的夹角为45°,他放出的风筝线长是30m,此时,他手距地面1.5米,你认为能否算出此时风筝的高度?若能,请你帮他算一算;若不能,请说明理由.
如图,小波在周末时随父母到郊外放风筝,已知风筝线与水平线的夹角为45°,他放出的风筝线长是30m,此时,他手距地面1.5米,你认为能否算出此时风筝的高度?若能,请你帮他算一算;若不能,请说明理由.
 如图,小波在周末时随父母到郊外放风筝,已知风筝线与水平线的夹角为45°,他放出的风筝线长是30m,此时,他手距地面1.5米,你认为能否算出此时风筝的高度?若能,请你帮他算一算;若不能,请说明理由.
如图,小波在周末时随父母到郊外放风筝,已知风筝线与水平线的夹角为45°,他放出的风筝线长是30m,此时,他手距地面1.5米,你认为能否算出此时风筝的高度?若能,请你帮他算一算;若不能,请说明理由.
5. 如图,在平面直角坐标系中,第一象限内长方形ABCD,AD∥x轴,点E在x轴上,EC交AD于G,BF平分∠CBE交OC于F,若∠CGD=2∠OCE,则下列结论正确的是( )
如图,在平面直角坐标系中,第一象限内长方形ABCD,AD∥x轴,点E在x轴上,EC交AD于G,BF平分∠CBE交OC于F,若∠CGD=2∠OCE,则下列结论正确的是( )
 如图,在平面直角坐标系中,第一象限内长方形ABCD,AD∥x轴,点E在x轴上,EC交AD于G,BF平分∠CBE交OC于F,若∠CGD=2∠OCE,则下列结论正确的是( )
如图,在平面直角坐标系中,第一象限内长方形ABCD,AD∥x轴,点E在x轴上,EC交AD于G,BF平分∠CBE交OC于F,若∠CGD=2∠OCE,则下列结论正确的是( )| A. | ∠BEC=∠BFO | B. | ∠BEC+∠BFO=135° | C. | $\frac{1}{2}$∠BEC+∠BFO=90° | D. | ∠BEC+$\frac{1}{2}$∠BFO=90° |
 如图,在三角形ABC中,BD:DC=5:7,AE:ED=3:5,EF:FC=2:3,三角形ABC的面积是56cm2,那么三角形DEF的面积是多少?
如图,在三角形ABC中,BD:DC=5:7,AE:ED=3:5,EF:FC=2:3,三角形ABC的面积是56cm2,那么三角形DEF的面积是多少? 如图是一个直角边长为2的等腰直角三角形,建立适当的直角坐标系xOy,写出各个顶点的坐标.
如图是一个直角边长为2的等腰直角三角形,建立适当的直角坐标系xOy,写出各个顶点的坐标. 如图,已知点A在∠EBF的角平分线上,C为AB的中点,CD∥BF,CD交BE于点D,
如图,已知点A在∠EBF的角平分线上,C为AB的中点,CD∥BF,CD交BE于点D,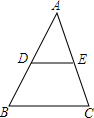 如图,已知$\frac{AD}{DB}=\frac{AE}{EC}=\frac{3}{2}$,求$\frac{AB}{DB}$,$\frac{EC}{AC}$,$\frac{AB}{AD}$.
如图,已知$\frac{AD}{DB}=\frac{AE}{EC}=\frac{3}{2}$,求$\frac{AB}{DB}$,$\frac{EC}{AC}$,$\frac{AB}{AD}$.