题目内容
8.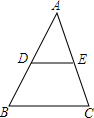 如图,已知$\frac{AD}{DB}=\frac{AE}{EC}=\frac{3}{2}$,求$\frac{AB}{DB}$,$\frac{EC}{AC}$,$\frac{AB}{AD}$.
如图,已知$\frac{AD}{DB}=\frac{AE}{EC}=\frac{3}{2}$,求$\frac{AB}{DB}$,$\frac{EC}{AC}$,$\frac{AB}{AD}$.
分析 根据如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边得到DE∥BC,然后根据平行线分线段成比例求解.
解答 解:∵$\frac{AD}{DB}=\frac{AE}{EC}=\frac{3}{2}$,
∴DE∥BC,
∴$\frac{AB}{DB}$=$\frac{5}{2}$,$\frac{EC}{AC}$=$\frac{5}{2}$,$\frac{AB}{AD}$=$\frac{5}{3}$.
点评 本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例;如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.也考查了比例的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
17.在+1,-2,-1这三个数中,任取两个数相加,所得的和最大的是( )
| A. | -1 | B. | 1 | C. | 0 | D. | -3 |
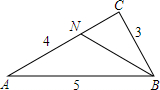 若BN为△ABC的角平分线,则sin∠CBN=$\frac{\sqrt{5}}{5}$,sin∠ABN=$\frac{\sqrt{5}}{5}$.
若BN为△ABC的角平分线,则sin∠CBN=$\frac{\sqrt{5}}{5}$,sin∠ABN=$\frac{\sqrt{5}}{5}$.