题目内容
4. 如图,在三角形ABC中,BD:DC=5:7,AE:ED=3:5,EF:FC=2:3,三角形ABC的面积是56cm2,那么三角形DEF的面积是多少?
如图,在三角形ABC中,BD:DC=5:7,AE:ED=3:5,EF:FC=2:3,三角形ABC的面积是56cm2,那么三角形DEF的面积是多少?
分析 由BD:DC=5:7,根据不同底等高的三角形面积的比等于底的比求得S△ACD=$\frac{7}{12}$×56=$\frac{98}{3}$,同理求得S△CDE=$\frac{5}{8}$×$\frac{98}{3}$=$\frac{245}{12}$,即可得到S△EDF=$\frac{2}{5}$×$\frac{245}{12}$=$\frac{49}{6}$.
解答 解:∵BD:DC=5:7,
∴CD:BC=7:12,
∵三角形ABC的面积是56cm2,
∴S△ACD=$\frac{7}{12}$×56=$\frac{98}{3}$,
∵AE:ED=3:5,
∴DE:AD=5:8,
∴S△CDE=$\frac{5}{8}$×$\frac{98}{3}$=$\frac{245}{12}$,
∵EF:FC=2:3,
∴EF:CE=2:5,
∴S△EDF=$\frac{2}{5}$×$\frac{245}{12}$=$\frac{49}{6}$.
点评 本题考查的是三角形面积的计算,熟知不同底等高的三角形面积的比等于底的比是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.某校图书馆上周借书记录(超过100册的部分记为正,少于100册的部分记为负)如下表:
(1)上星期五借出多少册书?
(2)上星期借书最多的一天比借书最少的一天多借出图书多少册?
(3)上星期平均每天借出多少册书?
| 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
| +18 | -6 | +15 | 0 | -12 |
(2)上星期借书最多的一天比借书最少的一天多借出图书多少册?
(3)上星期平均每天借出多少册书?
14.已知直线l,在l上取一点A,经过点A与l相切且半径为5cm的圆有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图所示,在四边形ABCD中,∠ABC=∠ADC=90°,P是对角线AC的中点,Q是对角线BD的中点,求证:PQ⊥BD.
如图所示,在四边形ABCD中,∠ABC=∠ADC=90°,P是对角线AC的中点,Q是对角线BD的中点,求证:PQ⊥BD.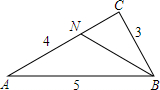 若BN为△ABC的角平分线,则sin∠CBN=$\frac{\sqrt{5}}{5}$,sin∠ABN=$\frac{\sqrt{5}}{5}$.
若BN为△ABC的角平分线,则sin∠CBN=$\frac{\sqrt{5}}{5}$,sin∠ABN=$\frac{\sqrt{5}}{5}$.