题目内容
5. 如图,在平面直角坐标系中,第一象限内长方形ABCD,AD∥x轴,点E在x轴上,EC交AD于G,BF平分∠CBE交OC于F,若∠CGD=2∠OCE,则下列结论正确的是( )
如图,在平面直角坐标系中,第一象限内长方形ABCD,AD∥x轴,点E在x轴上,EC交AD于G,BF平分∠CBE交OC于F,若∠CGD=2∠OCE,则下列结论正确的是( )| A. | ∠BEC=∠BFO | B. | ∠BEC+∠BFO=135° | C. | $\frac{1}{2}$∠BEC+∠BFO=90° | D. | ∠BEC+$\frac{1}{2}$∠BFO=90° |
分析 易证∠BCG=∠CGD=2∠OCE,由此可得∠BCF=∠GCF=$\frac{1}{2}$∠BCG.由BF平分∠CBE可得∠FBC=$\frac{1}{2}$∠CBE,根据三角形外角的性质可得∠BFO=∠FBC+∠BCF=$\frac{1}{2}$∠CBE+$\frac{1}{2}$∠BCG=90°-$\frac{1}{2}$∠BEC,问题得以解决.
解答 解: ∵四边形ABCD是矩形,
∵四边形ABCD是矩形,
∴BC∥AD,
∴∠BCG=∠CGD.
∵∠CGD=2∠OCE,
∴∠BCG=2∠OCE,
∴∠BCF=∠GCF=$\frac{1}{2}$∠BCG.
∵BF平分∠CBE,
∴∠FBC=$\frac{1}{2}$∠CBE,
∴∠BFO=∠FBC+∠BCF=$\frac{1}{2}$∠CBE+$\frac{1}{2}$∠BCG
=$\frac{1}{2}$(180°-∠BEC)
=90°-$\frac{1}{2}$∠BEC,
∴$\frac{1}{2}$∠BEC+∠BFO=90°.
故选C.
点评 本题主要考查了矩形的性质、角平分线的定义、三角形的外角性质、三角形内角和定理等知识,证到∠BCF=$\frac{1}{2}$∠BCG是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知直线l,在l上取一点A,经过点A与l相切且半径为5cm的圆有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.在+1,-2,-1这三个数中,任取两个数相加,所得的和最大的是( )
| A. | -1 | B. | 1 | C. | 0 | D. | -3 |
15.若132x=64,则13-x=( )
| A. | -$\frac{1}{8}$ | B. | ±$\frac{1}{8}$ | C. | $\frac{1}{80}$ | D. | $\frac{1}{512}$ |
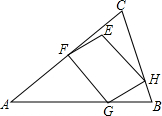 如图,在△ABC中,AB=AC=1,∠A=36°,?EFGH的顶点F,G,H分别在AC,AB,BC边上,且FC=CH.
如图,在△ABC中,AB=AC=1,∠A=36°,?EFGH的顶点F,G,H分别在AC,AB,BC边上,且FC=CH.