题目内容
1. 如图,已知点A在∠EBF的角平分线上,C为AB的中点,CD∥BF,CD交BE于点D,
如图,已知点A在∠EBF的角平分线上,C为AB的中点,CD∥BF,CD交BE于点D,(1)求证:DC=DB.
(2)连接AD,若AD⊥EB,求∠EBF的度数.
分析 (1)由BA平分∠EBF,得到∠EBA=∠FBA,根据平行线的性质得到∠DCB=∠CBG,等量代换得到∠DCB=∠DBC,于是得到结论;
(2)根据直角三角形的性质得到CD=BC,于是得到△CDB是等边三角形,即可得到结论.
解答 (1)证明:∵BA平分∠EBF,
∴∠EBA=∠FBA,
∵CD∥BF,
∴∠DCB=∠CBG,
∴∠DCB=∠DBC,
∴DC=BD;
(2)解:∵AD⊥BE,
∴∠ADB=90°,
∵C为AB的中点,
∴CD=BC,
∴△CDB是等边三角形,
∴∠DBC=60°,
∴∠EBF=120°.
点评 本题考查了等腰三角形的判定和性质,等边三角形的判定和性质,平行线的性质,直角三角形的性质,熟练掌握等腰三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
 如图所示,在四边形ABCD中,∠ABC=∠ADC=90°,P是对角线AC的中点,Q是对角线BD的中点,求证:PQ⊥BD.
如图所示,在四边形ABCD中,∠ABC=∠ADC=90°,P是对角线AC的中点,Q是对角线BD的中点,求证:PQ⊥BD.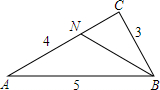 若BN为△ABC的角平分线,则sin∠CBN=$\frac{\sqrt{5}}{5}$,sin∠ABN=$\frac{\sqrt{5}}{5}$.
若BN为△ABC的角平分线,则sin∠CBN=$\frac{\sqrt{5}}{5}$,sin∠ABN=$\frac{\sqrt{5}}{5}$.