Question

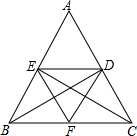已知BD平分∠ABC，BD交AC于点D，过D作DF∥AB交BC于点F，过F作EF∥AC交AB于点E，若四边形BEDF为平行四边形，求证：△ABC为等腰三角形．

Answer 1

考点：平行四边形的性质,等腰三角形的判定

专题：证明题,数形结合

分析：由BD平分∠ABC，四边形BEDF为平行四边形，易证得四边形BEDF为菱形，又由EF∥AC，易证得四边形CDEF是平行四边形，即可得DE=BF=BE=FC，则可得△BEF是等边三角形，△BCD与△BEC是直角三角形，继而证得结论．

解答：证明：∵BD平分∠ABC，
∴∠EBD=∠FBD，
∵四边形BEDF为平行四边形，
∴DE∥BC，BE=DF
∴∠EDB=∠FDB，
∴∠EBD=∠EDB，
∴EB=ED，
四边形BEDF为菱形，
∵EF∥AC，
∴四边形CDEF是平行四边形，
∴DE=FC，
∴DE=BF=BE=FC，
∴△BEF是等边三角形，△BCD与△BEC是直角三角形，
∴∠ABC=60°，
∴∠CBD=30°，
∴∠ACB=60°，
∴△ABC是等腰三角形．

点评：此题考查了平行四边形的性质、菱形的判定、等边三角形的判定与性质以及直角三角形的判定．此题难度适中，注意掌握数形结合思想的应用．