题目内容
已知x+y=5，xy=3，求：
（1）2x2+2y2；
（2）（x-y）2．
（1）2x2+2y2；
（2）（x-y）2．
考点：完全平方公式
专题：计算题
分析：根据完全平方公式（x+y）2=x2+2xy+y2，把原式变形：
（1）2x2+2y2=2（x+y）2-4xy，再把x+y、xy的值代入计算即可；
（2）（x-y）2=（x+y）2-4xy，再把x+y、xy的值代入计算即可．
（1）2x2+2y2=2（x+y）2-4xy，再把x+y、xy的值代入计算即可；
（2）（x-y）2=（x+y）2-4xy，再把x+y、xy的值代入计算即可．
解答：解：（1）∵x+y=5，xy=3，
∴2x2+2y2=2（x+y）2-4xy=2×52-4×3=38；
（2）∵x+y=5，xy=3，
∴（x-y）2=（x+y）2-4xy=52-4×3=13．
∴2x2+2y2=2（x+y）2-4xy=2×52-4×3=38；
（2）∵x+y=5，xy=3，
∴（x-y）2=（x+y）2-4xy=52-4×3=13．
点评：本题考查了完全平方公式，通过对公式的变形，达到灵活使用公式的目的．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
下列说法正确的是（ ）
| A、方程8x2-7=0的一次项系数为-7 |
| B、一元二次方程的一般形式是ax2+bx+c=0 |
| C、当k=0时，方程kx2+3x-1=x2为一元二次方程 |
| D、当m取所有实数时，关于x的方程（m2+1）x2-mx-3=0为一元二次方程 |
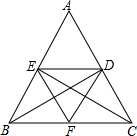已知BD平分∠ABC，BD交AC于点D，过D作DF∥AB交BC于点F，过F作EF∥AC交AB于点E，若四边形BEDF为平行四边形，求证：△ABC为等腰三角形．
AF平分∠BAC，P是AF上任意一点，过P向AB、AC作垂线PD、PE，D、E分别为垂足，连接DE．求证：AF垂直平分DE．