题目内容
不能判断四边形ABCD是矩形的是(0为对角线的交点)( )
| A、AB=CD,AD=BC,∠A=90° | ||
| B、OA=OB=OC=OD | ||
C、AB
| ||
D、AB
|
考点:矩形的判定
专题:
分析:矩形的判定定理有:
(1)有一个角是直角的平行四边形是矩形.
(2)有三个角是直角的四边形是矩形.
(3)对角线互相平分且相等的四边形是矩形.据此判断.
(1)有一个角是直角的平行四边形是矩形.
(2)有三个角是直角的四边形是矩形.
(3)对角线互相平分且相等的四边形是矩形.据此判断.
解答: 解:A、由“AB=CD,AD=BC”可以判定四边形ABCD是平行四边形,又∠BAD=90°,则根据“有一个角是直角的平行四边形是矩形”可以判定平行四边形ABCD是矩形,故本选项不符合题意;
解:A、由“AB=CD,AD=BC”可以判定四边形ABCD是平行四边形,又∠BAD=90°,则根据“有一个角是直角的平行四边形是矩形”可以判定平行四边形ABCD是矩形,故本选项不符合题意;
B、根据“对角线互相平分且相等的四边形是矩形”可以判定平行四边形ABCD是矩形,故本选项不符合题意;
C、根据AB
CD得到四边形是平行四边形,根据AC=BD,利用对角线相等的平行四边形是矩形,故本选项不符合题意;
D、只能得到四边形是平行四边形,故本选项符合题意;
故选:D.
 解:A、由“AB=CD,AD=BC”可以判定四边形ABCD是平行四边形,又∠BAD=90°,则根据“有一个角是直角的平行四边形是矩形”可以判定平行四边形ABCD是矩形,故本选项不符合题意;
解:A、由“AB=CD,AD=BC”可以判定四边形ABCD是平行四边形,又∠BAD=90°,则根据“有一个角是直角的平行四边形是矩形”可以判定平行四边形ABCD是矩形,故本选项不符合题意;B、根据“对角线互相平分且相等的四边形是矩形”可以判定平行四边形ABCD是矩形,故本选项不符合题意;
C、根据AB
| ∥ |
. |
D、只能得到四边形是平行四边形,故本选项符合题意;
故选:D.
点评:本题考查的是矩形的判定定理,但考生应注意的是由矩形的判定引申出来的各图形的判定.难度一般.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在一个直角三角形中,若斜边长为5cm,一条直角边的长为3cm,则另一条直角边的长为( )
| A、4cm | ||
B、4cm或
| ||
C、
| ||
| D、不存在 |
下列说法正确的是( )
| A、方程8x2-7=0的一次项系数为-7 |
| B、一元二次方程的一般形式是ax2+bx+c=0 |
| C、当k=0时,方程kx2+3x-1=x2为一元二次方程 |
| D、当m取所有实数时,关于x的方程(m2+1)x2-mx-3=0为一元二次方程 |
下列各式:①3
+3=6
;②
=1;③
+
=
=2
;④
=2
,其中错误的有( )
| 3 |
| 3 |
| 1 |
| 7 |
| 7 |
| 2 |
| 6 |
| 8 |
| 2 |
| ||
|
| 2 |
| A、3个 | B、2个 | C、1个 | D、0个 |
把a
中根号外的a移入根号内得( )
-
|
A、
| ||
B、
| ||
C、-
| ||
D、-
|
计算
+
-2x
的结果正确的是( )
| 2 |
| 3 |
| 9x |
|
|
A、3
| ||||
B、-3
| ||||
C、2
| ||||
D、
|
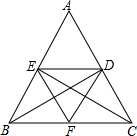 已知BD平分∠ABC,BD交AC于点D,过D作DF∥AB交BC于点F,过F作EF∥AC交AB于点E,若四边形BEDF为平行四边形,求证:△ABC为等腰三角形.
已知BD平分∠ABC,BD交AC于点D,过D作DF∥AB交BC于点F,过F作EF∥AC交AB于点E,若四边形BEDF为平行四边形,求证:△ABC为等腰三角形. AF平分∠BAC,P是AF上任意一点,过P向AB、AC作垂线PD、PE,D、E分别为垂足,连接DE.求证:AF垂直平分DE.
AF平分∠BAC,P是AF上任意一点,过P向AB、AC作垂线PD、PE,D、E分别为垂足,连接DE.求证:AF垂直平分DE.