题目内容
16. 如图,在矩形ABCD中,AB-BC=2,BD=4,则矩形ABCD的面积为3.
如图,在矩形ABCD中,AB-BC=2,BD=4,则矩形ABCD的面积为3.
分析 根据矩形的性质得出∠C=90°,DC=AB=x+2,在Rt△DCB中,根据勾股定理得出方程,求出x,即可求出答案.
解答 解:设BC=x,则AB=x+2,
∵四边形ABCD是矩形,
∴∠C=90°,DC=AB=x+2,
在Rt△DCB中,由勾股定理得:BD2=BC2+DC2,
即42=x2+(x+2)2,
解得:x=1(负数舍去),
∴BC=1,AB=1+2=3,
∴矩形ABCD的面积为AB×BC=3×1=3,
故答案为:3.
点评 本题考查了矩形的性质,勾股定理的应用,能根据矩形的性质进行推理是解此题的关键,注意:矩形的对边相等,矩形的每个角都是直角.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
6.下列尺规作图,能判断AD是△ABC边上的高是( )
| A. |  | B. |  | C. |  | D. |  |
7.若点(-3,y1),(-2,y2),(2,y3)都在反比例函数y=$\frac{3}{x}$的图象上,则( )
| A. | y1>y2>y3 | B. | y2>y1>y3 | C. | y3>y1>y2 | D. | y1>y3>y2 |
5. 菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=$\sqrt{2}$,BD=2,则菱形ABCD的面积为( )
菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=$\sqrt{2}$,BD=2,则菱形ABCD的面积为( )
 菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=$\sqrt{2}$,BD=2,则菱形ABCD的面积为( )
菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=$\sqrt{2}$,BD=2,则菱形ABCD的面积为( )| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 6$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
 小明参加某超市的翻笑脸抽奖活动,如图,四张笑脸背后分别对应价值50,100,100,200(单位:元)的代金券
小明参加某超市的翻笑脸抽奖活动,如图,四张笑脸背后分别对应价值50,100,100,200(单位:元)的代金券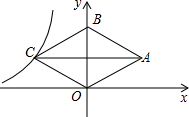 如图,菱形OABC的顶点O是原点,顶点B在y轴上,已知菱形的边长为5,一条对角线的长是6,反比例函数y=$\frac{k}{x}$(x<0)的图象经过顶点C,则k的值为-12.
如图,菱形OABC的顶点O是原点,顶点B在y轴上,已知菱形的边长为5,一条对角线的长是6,反比例函数y=$\frac{k}{x}$(x<0)的图象经过顶点C,则k的值为-12.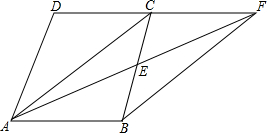 已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.
已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.