题目内容
4. 小明参加某超市的翻笑脸抽奖活动,如图,四张笑脸背后分别对应价值50,100,100,200(单位:元)的代金券
小明参加某超市的翻笑脸抽奖活动,如图,四张笑脸背后分别对应价值50,100,100,200(单位:元)的代金券(1)随机翻一张笑脸,抽中100元代金券的概率为$\frac{1}{2}$.
(2)随机翻两张笑脸,且第一次翻过的笑脸第二次不再翻,用列表法或画树状图的方法求所获代金券总价值为300元的概率.
分析 (1)由四张笑脸背后分别对应价值50,100,100,200(单位:元)的代金券,直接利用概率公式求解即可求得答案;
(2)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所获代金券总价值为300元的情况,再利用概率公式求解即可求得答案.
解答 解:(1)∵四张笑脸背后分别对应价值50,100,100,200(单位:元)的代金券,
∴随机翻一张笑脸,抽中100元代金券的概率为:$\frac{2}{4}$=$\frac{1}{2}$;
故答案为:$\frac{1}{2}$.
(2)画树状图得:
∵共有12种等可能的结果,所获代金券总价值为300元的有4种情况,
∴所获代金券总价值为300元的概率为:$\frac{4}{12}$=$\frac{1}{3}$.
点评 此题考查了列表法或树状图法求概率.注意此题属于不放回实验,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
相关题目
19. 小红要购买珠子串成一条手链,黑色珠子每个a元,白色珠子每个b元,要串成如图所示的手链,小红购买珠子应该花费( )
小红要购买珠子串成一条手链,黑色珠子每个a元,白色珠子每个b元,要串成如图所示的手链,小红购买珠子应该花费( )
 小红要购买珠子串成一条手链,黑色珠子每个a元,白色珠子每个b元,要串成如图所示的手链,小红购买珠子应该花费( )
小红要购买珠子串成一条手链,黑色珠子每个a元,白色珠子每个b元,要串成如图所示的手链,小红购买珠子应该花费( )| A. | (3a+4b)元 | B. | (4a+3b)元 | C. | 4(a+b)元 | D. | 3(a+b)元 |
14.若一个几何体的主视图、左视图、俯视图是半径相等的圆,则这个几何体是( )
| A. | 圆柱 | B. | 圆锥 | C. | 球 | D. | 正方体 |
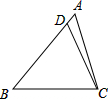 在△ABC中,D为AB边上一点,且∠BCD=∠A.已知BC=$2\sqrt{2}$,AB=3,则BD=$\frac{8}{3}$.
在△ABC中,D为AB边上一点,且∠BCD=∠A.已知BC=$2\sqrt{2}$,AB=3,则BD=$\frac{8}{3}$.
 如图,在矩形ABCD中,AB-BC=2,BD=4,则矩形ABCD的面积为3.
如图,在矩形ABCD中,AB-BC=2,BD=4,则矩形ABCD的面积为3.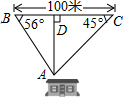 如图,为保护门源百里油菜花海,由“芬芳浴”游客中心A处修建通往百米观景长廊BC的两条栈道AB,AC.若∠B=56°,∠C=45°,则游客中心A到观景长廊BC的距离AD的长约为60米.(sin56°≈0.8,tan56°≈1.5)
如图,为保护门源百里油菜花海,由“芬芳浴”游客中心A处修建通往百米观景长廊BC的两条栈道AB,AC.若∠B=56°,∠C=45°,则游客中心A到观景长廊BC的距离AD的长约为60米.(sin56°≈0.8,tan56°≈1.5)