题目内容
6.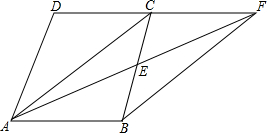 已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.
已知:如图,在四边形ABCD中,AB∥CD,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.
分析 利用平行线的性质得出∠BAE=∠CFE,由AAS得出△ABE≌△FCE,得出对应边相等AE=EF,再利用平行四边形的判定得出即可.
解答 解:四边形ABFC是平行四边形;理由如下:
∵AB∥CD,
∴∠BAE=∠CFE,
∵E是BC的中点,
∴BE=CE,
在△ABE和△FCE中,$\left\{\begin{array}{l}{∠BAE=∠CFE}&{\;}\\{∠AEB=∠FEC}&{\;}\\{BE=CE}&{\;}\end{array}\right.$,
∴△ABE≌△FCE(AAS);
∴AE=EF,
又∵BE=CE
∴四边形ABFC是平行四边形.
点评 此题主要考查了平行四边形的判定、全等三角形的判定与性质等知识;熟练掌握平行四边形的判定方法,证明三角形全等是解决问题的关键.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案
相关题目
17.(-2)3=( )
| A. | -6 | B. | 6 | C. | -8 | D. | 8 |
14.若一个几何体的主视图、左视图、俯视图是半径相等的圆,则这个几何体是( )
| A. | 圆柱 | B. | 圆锥 | C. | 球 | D. | 正方体 |
4.将根号外的式子移到根号内:m$\sqrt{-\frac{1}{m}}$=( )
| A. | $\sqrt{-m}$ | B. | -$\sqrt{m}$ | C. | -$\sqrt{-m}$ | D. | 1 |
8. 如图,Rt△OAB的顶点O与坐标原点重合,∠AOB=90°,AO=2BO,当点A在反比例函数y=$\frac{2}{x}$(x>0)的图象上移动时,点B的坐标满足的函数解析式为( )
如图,Rt△OAB的顶点O与坐标原点重合,∠AOB=90°,AO=2BO,当点A在反比例函数y=$\frac{2}{x}$(x>0)的图象上移动时,点B的坐标满足的函数解析式为( )
 如图,Rt△OAB的顶点O与坐标原点重合,∠AOB=90°,AO=2BO,当点A在反比例函数y=$\frac{2}{x}$(x>0)的图象上移动时,点B的坐标满足的函数解析式为( )
如图,Rt△OAB的顶点O与坐标原点重合,∠AOB=90°,AO=2BO,当点A在反比例函数y=$\frac{2}{x}$(x>0)的图象上移动时,点B的坐标满足的函数解析式为( )| A. | y=-$\frac{1}{x}$(x<0) | B. | y=-$\frac{1}{2x}$(x<0) | C. | y=-$\frac{1}{4x}$(x<0) | D. | y=-$\frac{1}{8x}$(x<0) |
 如图,在矩形ABCD中,AB-BC=2,BD=4,则矩形ABCD的面积为3.
如图,在矩形ABCD中,AB-BC=2,BD=4,则矩形ABCD的面积为3. 为了推动校园足球发展,某市教体局准备向全市中小学免费赠送一批足球,这批足球的生产任务由甲、乙两家足球制造企业平均承担,甲企业库存0.2万个,乙企业库存0.4万个,两企业同时开始生产,且每天生产速度不变,甲、乙两家企业生产的足球数量y万个与生产时间x天之间的函数关系如图所示,则每家企业供应的足球数量a等于1万个.
为了推动校园足球发展,某市教体局准备向全市中小学免费赠送一批足球,这批足球的生产任务由甲、乙两家足球制造企业平均承担,甲企业库存0.2万个,乙企业库存0.4万个,两企业同时开始生产,且每天生产速度不变,甲、乙两家企业生产的足球数量y万个与生产时间x天之间的函数关系如图所示,则每家企业供应的足球数量a等于1万个.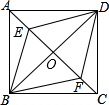 如图,已知正方形ABCD的对角线交于O点,点E、F分别是AO、CO的中点,连接BE、BF、DE、DF,则下列结论中一定成立的是①③④(把所有正确结论的序号都填在横线上)
如图,已知正方形ABCD的对角线交于O点,点E、F分别是AO、CO的中点,连接BE、BF、DE、DF,则下列结论中一定成立的是①③④(把所有正确结论的序号都填在横线上)