题目内容
18.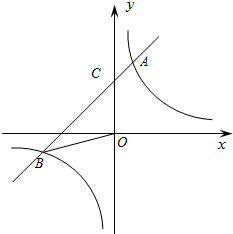 如图,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1).
如图,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1).(1)分别求出反比例函数与一次函数的函数关系式;
(2)若一次函数与y轴相交于点C,求△BOC的面积;
(3)观察图象请直接写出:一次函数的值大于反比例函数的值的自变量的取值范围.
分析 (1)根据待定系数法就可以求出函数的解析式;
(2)求△BOC的面积就是求B,C两点的坐标.
(3)由图象可直接观察出一次函数的值大于反比比例函数的值时x的取值范围.
解答 解:(1)∵点A(1,3)在反比例函数图象上
∴k=3
即反比例函数关系式为y=$\frac{3}{x}$;
∵点B(n,-1)在反比例函数图象上
∴n=-3
∵点A(1,3)和B(-3,-1)在一次函数y=mx+b的图象上
∴$\left\{\begin{array}{l}{m+b=3}\\{-3m+b=-1}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=1}\\{b=2}\end{array}\right.$.
∴一次函数关系式为y=x+2
(2)当x=0时,一次函数值为2
∴OC=2
∴S△BOC=$\frac{1}{2}$×2×|-3|=3.
(3)由图可知,在A点右侧时,或在B点右侧y轴左侧时,一次函数的值大于反比比例函数的值,
此时x>1或-3<x<0.
点评 本题考查了反比例函数与一次函数的交点问题及待定系数法求函数解析式,要注意结合图形的性质并挖掘图形提供的隐含条件.

练习册系列答案
相关题目
6. 如图,一次函数y=(m+2)x+(1-m)经过一、二、四象限,则m的取值范围是( )
如图,一次函数y=(m+2)x+(1-m)经过一、二、四象限,则m的取值范围是( )
 如图,一次函数y=(m+2)x+(1-m)经过一、二、四象限,则m的取值范围是( )
如图,一次函数y=(m+2)x+(1-m)经过一、二、四象限,则m的取值范围是( )| A. | m<-2 | B. | m<1 | C. | -2<m<1 | D. | m>-2 |
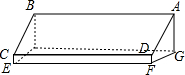 “蔬菜大王“老杨建造了一个育苗温室(如图).温室南墙高DF=0.3m,北墙高AG=1.6m,温室下底面是长方形,长EF=8m,宽FG=3m,求温室玻璃盖ABCD的面积(结果保留一位小数).
“蔬菜大王“老杨建造了一个育苗温室(如图).温室南墙高DF=0.3m,北墙高AG=1.6m,温室下底面是长方形,长EF=8m,宽FG=3m,求温室玻璃盖ABCD的面积(结果保留一位小数).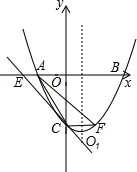 如图,抛物线y=ax2+bx+c(a>0)的顶点为O1,与x轴相交于A、B两点,与y轴相交于点C,A、B两点的坐标分别为(-1,0)和(3,0),且OB=OC.
如图,抛物线y=ax2+bx+c(a>0)的顶点为O1,与x轴相交于A、B两点,与y轴相交于点C,A、B两点的坐标分别为(-1,0)和(3,0),且OB=OC.
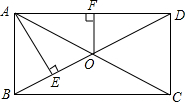 如图,在矩形ABCD中,AE⊥BD于点E,BE=OE,过两条对角线的交点O作OF⊥AD,且OF=2,求BD的长.
如图,在矩形ABCD中,AE⊥BD于点E,BE=OE,过两条对角线的交点O作OF⊥AD,且OF=2,求BD的长.