题目内容
9.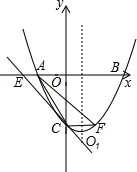 如图,抛物线y=ax2+bx+c(a>0)的顶点为O1,与x轴相交于A、B两点,与y轴相交于点C,A、B两点的坐标分别为(-1,0)和(3,0),且OB=OC.
如图,抛物线y=ax2+bx+c(a>0)的顶点为O1,与x轴相交于A、B两点,与y轴相交于点C,A、B两点的坐标分别为(-1,0)和(3,0),且OB=OC.(1)求抛物线的解析式;
(2)设直线CO1与x轴相交于点E,过点C作CF∥x轴与抛物线相交于点F.求证:四边形AECF是平行四边形.
分析 (1)先利用OB=OC确定C(0,-3),再设交点式y=a(x+1)(x-3),然后把C点坐标代入求出a即可得到抛物线解析式;
(2)先把(1)中的解析式配成顶点式得到顶点为O1的坐标为(1,-4),再利用待定系数法求出直线CO1的解析式为y=-x-3,则可得到E(0,-3),所以AE=2,接着利用点C(0,-3)与点F关于直线x=1对称得到CF=2,所以AE=CF,然后根据平行四边形的判定方法可判断四边形AECF是平行四边形.
解答 (1)解:∵B(3,0),
∴OB=3,
而OC=OB,
∴C(0,-3),
设抛物线解析式为y=a(x+1)(x-3),
把C(0,-3)代入得a•1•(-3)=-3,解得a=1,
∴抛物线解析式为y=(x+1)(x-3),即y=x2-2x-3;
(2)证明:∵y=x2-2x-3=(x-1)2-4,
∴顶点为O1的坐标为(1,-4),
设直线CO1的解析式为y=mx+n,
把C(0,-3)、O1(1,-4)代入得$\left\{\begin{array}{l}{n=-3}\\{m+n=-4}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=-1}\\{n=-3}\end{array}\right.$,
∴直线CO1的解析式为y=-x-3,
当y=0时,y=-x-3=-3,则E(0,-3),
∴AE=-1-(-3)=2,
∵CF∥x轴,
∴点C(0,-3)与点F关于直线x=1对称,
∴CF=2,
∴AE=CF,
而AE∥CF,
∴四边形AECF是平行四边形.
点评 本题考查了二次函数综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和平行四边形的判定;会利用待定系数法求二次函数和一次函数解析式;理解坐标与图形性质.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 若平行四边形ABCD的面积为24cm2,则三角形ABO的面积为( )cm2.
若平行四边形ABCD的面积为24cm2,则三角形ABO的面积为( )cm2.| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
3x-1,a=4,S=100t+5,5xy-3,4mn,2-b>6,-2,7x2+8x-1.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,在平面直角坐标系中,有两条抛物线,它们的对称轴相同,则下列关系中,不正确的是( )
如图,在平面直角坐标系中,有两条抛物线,它们的对称轴相同,则下列关系中,不正确的是( )| A. | m=k | B. | m=h | C. | k>n | D. | h<0,n>0 |
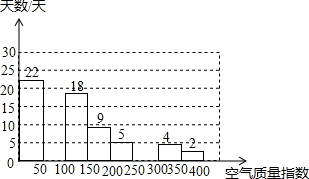 为了解空气质量情况,河北省某市从环境检测网随机抽取了2015年100天的空气质量指数,绘制了如图所示的统计表和如图所示的不完整的频数分布直方图,请你根据图表中提供的信息,解答下面的问题.
为了解空气质量情况,河北省某市从环境检测网随机抽取了2015年100天的空气质量指数,绘制了如图所示的统计表和如图所示的不完整的频数分布直方图,请你根据图表中提供的信息,解答下面的问题. | 级别 | 空气质量指数 | 天数 |
| 优 | 0-50 | 22 |
| 良 | 51-100 | m |
| 轻度污染 | 101-150 | 18 |
| 中度污染 | 151-200 | 9 |
| 重度污染 | 201-300 | 15 |
| 严重污染 | 301-400 | 6 |
(2)在图中,空气质量指数的众数位于优级别的;
(3)长期在外地工作的王兵因家中有事返家,求他到家的当天恰好空气质量指数不高于150的概率.
 如图,某同学站在旗杆正对的教学楼上点C处观测到旗杆顶端A的仰角为30°,旗杆底端B的俯角为45°,已知旗杆距离教学楼12米,求旗杆AB的高度.
如图,某同学站在旗杆正对的教学楼上点C处观测到旗杆顶端A的仰角为30°,旗杆底端B的俯角为45°,已知旗杆距离教学楼12米,求旗杆AB的高度.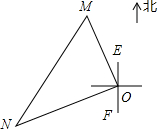 一艘轮船和一艘渔船同时沿各自的航向从港口O出发,如图所示,轮船从港口O沿北偏西20°的方向行60海里到达点M处,同一时刻渔船已航行到与港口O相距80海里的点N处,若M、N两点相距100海里,则∠NOF的度数为( )
一艘轮船和一艘渔船同时沿各自的航向从港口O出发,如图所示,轮船从港口O沿北偏西20°的方向行60海里到达点M处,同一时刻渔船已航行到与港口O相距80海里的点N处,若M、N两点相距100海里,则∠NOF的度数为( )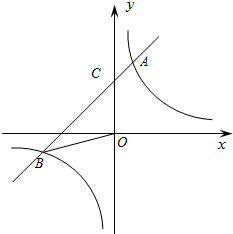 如图,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1).
如图,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1). 如图,在四边形ABCD中,E、F、G、H分别是各边的中点,对角线AC⊥BD于点O.求证:四边形EFGH是矩形.
如图,在四边形ABCD中,E、F、G、H分别是各边的中点,对角线AC⊥BD于点O.求证:四边形EFGH是矩形.