题目内容
10.观察下列算式:①42-22=12×1 ②72-52=12×2
③102-82=12×3 ④132-112=12×4
…
(1)请你按以上规律写出第4个算式;
(2)把这个规律用含字母的式子表示出来;
(3)你认为(2)中所写出的式子一定成立吗?并说明理由.
分析 (1)根据已知3个等式知,等式左边是序数的3倍加1与序数的3倍减1的平方差,等式右边是序数的12倍,据此规律可写出第4个等式;
(2)根据(1)中规律,列出第n个等式即可;
(3)将(2)中等式左边按照平方差公式化简,判断与等式右边是否相等即可.
解答 解:(1)∵第①个等式是:42-22=12×1,即(3×1+1)2-(3×1-1)2=12×1;
第②个等式是:72-52=12×2,即(3×2+1)2-(3×2-1)2=12×2;
第③个等式是:102-82=12×3,即(3×3+1)2-(3×3-1)2=12×3;
∴第④个等式是:(3×4+1)2-(3×4-1)2=12×4,即132-112=12×4;
(2)根据(1)中规律,知第n个式子为:(3n+1)2-(3n-1)2=12n;
(3)一定成立,理由如下:
∵左边=[(3n+1)-(3n-1)][(3n+1)+(3n-1)]=2×6n=12n,右边=12n,
∴左边=右边,
∴(3n+1)2-(3n-1)2=12n一定成立.
点评 本题主要考查发现数字的变化规律的能力,发现等式变化前后相同部分和变化部分是根本,而发现变化部分如何变化是寻找普遍规律的关键,将规律用代数式表示出来并验证是考查整式运算的一项重要技能.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.下列各式中代数式的个数有( )
3x-1,a=4,S=100t+5,5xy-3,4mn,2-b>6,-2,7x2+8x-1.
3x-1,a=4,S=100t+5,5xy-3,4mn,2-b>6,-2,7x2+8x-1.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
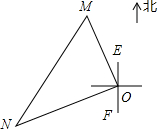 一艘轮船和一艘渔船同时沿各自的航向从港口O出发,如图所示,轮船从港口O沿北偏西20°的方向行60海里到达点M处,同一时刻渔船已航行到与港口O相距80海里的点N处,若M、N两点相距100海里,则∠NOF的度数为( )
一艘轮船和一艘渔船同时沿各自的航向从港口O出发,如图所示,轮船从港口O沿北偏西20°的方向行60海里到达点M处,同一时刻渔船已航行到与港口O相距80海里的点N处,若M、N两点相距100海里,则∠NOF的度数为( )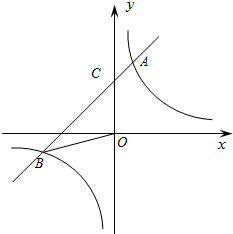 如图,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1).
如图,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=mx+b的图象相交于两点A(1,3),B(n,-1). 如图,△ABC绕点O按逆时针方向旋转后,顶点A旋转到了点D.
如图,△ABC绕点O按逆时针方向旋转后,顶点A旋转到了点D. 如图,直线l∥x轴,分别与函数$y=\frac{2}{x}$(x>0)和$y=\frac{k}{x}$(x<0)的图象相交于点A、B,交y轴于点C,若AC=2BC,则k=-1.
如图,直线l∥x轴,分别与函数$y=\frac{2}{x}$(x>0)和$y=\frac{k}{x}$(x<0)的图象相交于点A、B,交y轴于点C,若AC=2BC,则k=-1. 如图.∠1+∠2+∠3+∠4+∠5+∠6的值为720°(分割成三角形).
如图.∠1+∠2+∠3+∠4+∠5+∠6的值为720°(分割成三角形). 如图,在四边形ABCD中,E、F、G、H分别是各边的中点,对角线AC⊥BD于点O.求证:四边形EFGH是矩形.
如图,在四边形ABCD中,E、F、G、H分别是各边的中点,对角线AC⊥BD于点O.求证:四边形EFGH是矩形.